(Megjegyzés: ez a bejegyzés a régi Mi a különbség az "után" és a "következtében" között...? és a Kis kitérő az anekdotikus bizonyítékokhoz bejegyzések egybeszerkesztett változata. A tartalom nem változott, csak a két írást – mivel logikailag összetartoznak, hasonló témát tárgyalnak – összeszerkesztettem egy posztba.)
Ez a pont tulajdonképpen a 'korreláció nem implikál kauzalitást' egy újabb körüljárása lesz – ám más, de a gyakorlatban nagyon is fontos szempontok alapján.
A mellékhatások megítélésekor, ez általában is így van minden gyógyszernél, állandó problémát jelent annak eldöntése, hogy egy adott, gyógyszerbevitelt követő – nemkívánatos – esemény a gyógyszer miatt következett-e be (mert nyilván csak ekkor nevezhetjük egyáltalán "mellékhatásnak", hiszen különben már a "hatás" szó használata sem jogos), vagy csak véletlenül lépett fel pont a gyógyszer bevitele után. Különösen, ha ez az esemény nem az alany halálozása volt (azaz egyrészt nincs mód felboncolni, másrészt a motiváció is kisebb, hogy nagyon alaposan utánajárjunk az esetnek), akkor nagyon nehéz, néha pedig egyenesen lehetetlen feladat egyes esetekben nyilatkozni arról, hogy volt-e ok-okozati összefüggés a gyógyszer bevitele és az esemény között. Bevettem egy aszpirint és három órára rá megfájdult a fejem – ugyan ki a fene tudja megmondani (és hogyan?), hogy az aszpirin váltotta ki a fejfájásomat, vagy az akkor is bekövetkezett volna, ha be sem veszem…? Sokszor az ilyen kérdések egyetlen megbízható vizsgálati módszere az időgép alkalmazása: visszamegyünk az időben, nem vesszük be a gyógyszert, és megnézzük mi történik. Ha viszont véletlenül pont nincs kéznél időgép, akkor egyetlen lehetőség marad: epidemiológiai adatokra támaszkodni. Például egy kontrollált klinikai kísérletre, ahol alanyokat (lehetőleg elég nagy számút) lehetőleg véletlenszerűen két csoportba sorolunk úgy, hogy az egyik aszpirint kap, a másik ugyanolyan tablettát aszpirin nélkül (lehetőleg úgy, hogy sem az orvosok, sem a betegek nem tudják, hogy ki mit kap), majd feljegyezzük, hogy az egyes csoportokban milyen arányban jelentkezett fejfájás. Ez a legjobb módszer; csak sajnos a konkrét esetek megválaszolásában nem segít – legalábbis közvetlenül. Közvetetten nyilván igen, mert ha a fenti kísérletek azt az eredményt hozták, hogy a gyógyszert kapó csoportban nem gyakoribb a fejfájás, akkor joggal mondhatom, hogy minden bizonnyal konkrétan az én fejfájásom sem a gyógyszer miatt volt. Ez viszont egy fontos gondolat! Sokan kevésbé hajlandóak elfogadni egy ilyen okfejtést, pedig az előzőek értelmében teljesen racionális, és gyakran csak ilyenekre lehet támaszkodni egy olyan kérdés megválaszolásában, hogy vajon adott eseményt a gyógyszer okozott-e.
A problémát épp az jelenti, hogy ilyen események, a fejfájástól a halálozásig minden, természetesen bekövetkeznek gyógyszerbevitel nélkül is, így egyes, konkrét esetekben nehéz elkülöníteni a véletlen egybeesést az okozatiságtól. Bizonyos esetekben lehetséges ugyan orvosi alapon eldönteni a kérdést (pl. a kanyaró oltás után jelentkező agyvelőgyulladásról kiderül, hogy kullancsterjesztette encephalitis – ez egy konkrét magyarországi eset), ám erre sokszor nem lehet számítani. Ettől még tény, hogy az epidemiológiai adatokon kívül érdemes lehet a kérdést orvosi szempontból is megvizsgálni, olyan szemmel, hogy egyáltalán elképzelhető-e, hogy a vakcina adott hatást váltson ki, létezhet-e mechanizmus, ami révén az oltás beadása egyáltalán tud olyan mellékhatást okozni, mint amit vizsgálunk. Ezt a kérdést szokták biológiai plauzibilitásnak nevezni, az ilyen vizsgálatokat pedig – megkülönböztetésül az epidemiológiai vizsgálatoktól – mechanisztikus vizsgálatnak. Ezzel a továbbiakban nem foglalkozom, mert orvosi szakismereteket igénylő kérdésről van szó. Az egyetlen nem-orvosi jellegű fogódzkodót az időbeli egybeesés (szép szóval: temporális asszociáció) szorossága jelentheti: sokkal gyanúsabb a helyzet, ha az aszpirin bevétele után negyedórával fájdult meg a fejem, mint ha két hétre rá.
De még ezzel együtt is: 'korreláció nem implikál kauzalitást' elve – erre az esetre alkalmazva – épp azt mondja ki, hogy az, hogy az esemény a gyógyszer bevitele után következett be, önmagában nem igazolja, hogy az egy mellékhatás (azaz hogy a gyógyszer okozta is). Ezt az – általában is megfogalmazható – logikai tévedést szokás "post hoc ergo propter hoc" ("utána volt tehát miatta volt") típusú következtetési hibának nevezni.
Ez a probléma különösen gyakran kerülhet elő olyan készítményeknél, melyeket széleskörben alkalmaznak, hiszen ez a véletlen egybeesések valószínűségét is megnöveli. Márpedig a védőoltásokra ez a feltétel ugyancsak megvalósul. Kissé extrém példaként azt mondhatom, hogy ha 1 hónapos intervallumot tekintünk "gyanúsnak", akkor minden magyar gyermek minden első élethónapban bekövetkezett nemkívánatos eseményéért lehetne a BCG-oltást okolni...
Részben emiatt is ez a kérdéskör számos manipulációra ad lehetőséget, amit a védőoltás-ellenesek – természetesen – ki is használnak. Itt néhány ilyet szeretnék kicsit részletesebben is megnézni több a védőoltásokkal kapcsolatos konkrét példán keresztül.
Mielőtt igazából belevágunk, könnyedebb hangvételű felvezetésként hadd kezdjek egy – félig valós – párbeszéddel, amely köztem (FT) és egy védőoltás-ellenes (VE) között zajlott:
- VE [Gúnyosan] Na jó, de akkor ha ezeket nem hiszed el, hadd kérdezzelek meg: szerinted mennyi annak a valószínűsége, hogy valaki meghal a DTP-oltás beadása után?
- FT 100%.
- VE Na ugye, megm… ööö… hogy mit mondtál?
- FT Azt, hogy 100%.
- VE Tessék?? Hány százalék?
- FT 100.
- VE Huh. Hát… Szóval megtörtél! Bevallod?!
- FT Igen, álláspontom szerint 100% a halálozás valószínűsége a DTP-oltás után.
- VE És hát… ez pontosan amúgy mire alapozva jött ki?
- FT Nagyon egyszerű. A tudomány jelenlegi állása szerint (előbb vagy utóbb) de minden ember meghal. A halálozás valószínűsége tehát minden emberre nézve 100%. Jelenlegi ismereteink szerint ez alól a DTP-oltottak csoportja sem képez kivételt – így annak a valószínűsége, hogy valaki a DTP-oltásban részesülés után meg fog halni, 100%...
Nem tudom megállni, hogy le ne írjak egy másik esetet is, amibe nemrég futottam bele. Interneten láttam egy védőoltás-ellenes képet, ami azt állította, hogy az egyik HPV elleni védőoltás esetében már a vakcina klinikai kísérlete során is 21-en haltak bele az oltásba. Amikor ezt láttam, fogtam magam, és megkerestem az oltás tájékoztatóját (ami volt vagy 30 másodperc – filozófiai kérdés: vajon ezt hányan tették meg a képet megnézők közül? hányan háborodtak fel anélkül, hogy akár csak megpróbálták volna az állítást ellenőrizni? és közülük hányan küldték tovább minden ismerősüknek...?), és – figyelem! – kiderült, hogy az állítás tökéletesen helytálló. Valóban így történt, az oltott csoportban pontosan 21 haláleset fordult elő, feketén-fehéren ez volt leírva a hivatalos tájékoztatóban is.
...esetleg talán csak annyival érdemes a fenti információt árnyalni, hogy ha tovább olvasunk, akkor az is kiderül, hogy mibe haltak bele. Íme a három leggyakoribb halálok: 1) gépjármű-baleset 2) kábítószer-túladagolás/szándékos önártalom 3) lőfegyver okozta sérülés...
Remélem ezek a példák is jól mutatják, hogy mennyire nem mindegy, hogy egy esemény a védőoltás beadása után történik, vagy a védőoltás beadásának következtében történik…
Vágjunk akkor bele!
Időbeli egybeesés és ok-okozatiság
Első konkrét példánk a HPV-oltáshoz kapcsolódik. (Ez ugyan nem életkorhoz kötött kötelező oltás, de mostani mondanivalóm illusztrációjaként tökéletesen megfelel.) Ennek kapcsán ugyanis kering a neten egy lista, amelyet egyes védőoltás-ellenes oldalak úgy mutatnak be, mint az oltás mellékhatásainak "hivatalos" felsorolását. Íme:

Azt gondolom, hogy akadémiai tagság nélkül, pusztán józan paraszti ésszel is adódik két kérdés a derék védőoltás-ellenesekhez, akik fapofával kirakják ezt, mint a "mellékhatások" (ráadásul "hivatalos") listája:
- Nem gyanús egy egész leheletnyit, hogy ugyanaz a szer képes lényegében az összes szervrendszerünkben a legkülönfélébb, egymással semmilyen hasonlóságot nem mutató jelenségeket kiváltani…? Egy hangyányit sem furcsa, hogy egyszerre okozhat vakságot, pánikrohamot, fényérzékenységet, kiütéseket, személyiségváltozást, húgyúti fertőzést, fogfájást, elmosott beszédet, vérhányást, diszlexiát, hátfájást, korai menopauzát, szürke (nem is más színű!) bevonatot a fogakon és puffadást?! Ezt mind?! Ugyanaz a szer?! Hát könyörgöm. Ha szándékosan kellene gyártani valamit, ami ezeket mind tudja okozni, az is lehetetlen lenne… Ismétlem, ennek a csillagászati abszurditása szerintem józan paraszti ésszel is tökéletesen belátható; inkább az a felfoghatatlan számomra, hogy bárki komolyan vesz egy ilyen listát, és a felénél nem röhögi el magát.
- Egész picit sem furcsa a védőoltás-elleneseknek, hogy a listán szerepelnek egymással teljesen ellentétes hatások is?! Egyszerre okozhat súlyvesztést és súlynövekedést, hasmenést és székrekedést? Ez sem gyanús egy egész kicsit sem?
Gondolom a fentiek fényében nem árulok el nagy meglepetést: ez természetesen nem a HPV-oltás mellékhatásainak a listája. Aki ilyet állít, az egész egyszerűen hazudik.
A valóságban ez a lista azt tartalmazza, hogy milyen eseményeket jelentettek a HPV-oltás után. (Ráadásul egy egy önkéntes, a bejelentéseket nem ellenőrző jelentőrendszeren, a VAERS-en keresztül. Ez tovább árnyalja a képet, hiszen az egész most következő okfejtésem akkor is helytálló, ha az ilyen jelentések teljesen hitelesek, de itt ráadásul ez is megkérdőjelezhető: jelentést akár a beteg is beküldhet, mindenféle ellenőrzés nélkül. Ennek elég jól látható az eredménye a listán, gondolok az olyan leírásokra, mint "véletlenszerű rángatózás a végtagokban", "vegyi érzékenység", "agyi köd", de a személyes kedvencem az "érzékenység a kereskedelmileg feldolgozott citromsavra" (a nem-kereskedelmileg feldolgozott citromsavra tehát nyilván nem tesz érzékenyebbé a HPV-oltás, ügyes!). Márpedig az, hogy egyesek szerint a HPV-oltás, mint általában minden oltás, a halálozásig bezárólag kb. akármit okozhat, nem jelenthet semmiféle újdonságot azoknak, akik valaha láttak védőoltás-ellenes weboldalt… Ilyen szempontból tehát a listán nem sok meglepetés van.
A kérdés tehát, hogy ezek közül melyik az, amelyik valóban mellékhatásnak nevezhető. Nem azt mondom, hogy egyik se, csak azt, hogy erről a fenti lista semmit nem mond – még akár az is lehet, hogy az összes valóban mellékhatás, de ez a fajta adatgyűjtés ezt akkor sem bizonyítja. Ilyen események, hasmenéstől a halálozásig, ugyanis bekövetkeznek akkor is, ha az ember nem HPV-oltást kapott éppen (ezt talán senki nem vitatja…), innentől kezdve pedig nem tudhatjuk, hogy a fentiekből melyik az, ami amúgy is bekövetkezett volna, és melyik az, ami valóban ok-okozati kapcsolatba hozható az oltással.
Hiszen ne feledjük: az oltásnak (vagy egyáltalán: bármilyen beavatkozásnak) nem akkor van kockázata, ha utána bekövetkeznek nemkívánatos események, hanem akkor, ha több következik be, mint amennyi az oltás nélkül bekövetkezett volna! Nem a kockázat a kérdés, hanem az – esetleges – kockázatnövekedés.
Itt érünk el ahhoz a ponthoz, ahol – ismét – kibukik, hogy miért vannak a védőoltás-ellenesek manipulációi komoly lépéselőnyben az igazsággal szemben a média mai szemlélete mellett. Mert mi lenne a racionális reakció a fenti listára? Természetesen nem az, hogy dobjuk ki a kukába, mert nem ér semmit! (Nyilván, különben nem működtetnék a VAERS-t…) Egy ilyen adatgyűjtés egyáltalán nem felesleges, sőt, nagyon is szükséges – mégpedig "tippadó" adatbázisként! Az oltás utáni nemkívánatos eseményeket igenis szükséges a lehető legalaposabban, átlátható módon gyűjteni (ez az ún. posztmarketing vizsgálat, avagy farmakovigilancia, "fázis-IV"), hiszen a törzskönyvezés során ki nem derült, esetleges valódi mellékhatások gyanúját ez vetheti fel. Amennyiben ilyen felmerül, akkor az – például a fejfájós esetben említett kontrollált kísérlettel, vagy más, alkalmas módon, ahogy arról még lesz szó – célirányosan vizsgálható, hogy eldöntsük, valóban mellékhatásról van-e szó. E kérdésekről a védőoltások biztonságának valódi vizsgálati módszerei kapcsán fogok részletesebben beszélni. Na de ezt követelik a védőoltás-ellenesek a listát látva? Ugyan már, sokkal egyszerűbb célra használják ezt: az emberek ijesztgetésére. Rosszabb verziójában: lehet menni turnézni a tévébe, rádióba, mutogatni, hogy Pistike agyi ködöt kapott, vért hány és érzékeny lett a kereskedelmileg feldolgozott citromsavra az oltás következtében. Ezzel a stratégiával rettenetesen nehéz felvenni a versenyt. Kínos alapossággal be lehet mutatni Pistike szerencsétlen életét, sírdogáló anyuka stb., és a végén csak annyit kell mondani: mindez a védőoltás beadása után 3 nappal történt. A hatás – sajnos – szinte garantálható; tudják is ezt az érzelmekre apelláló manipulátorok.
Pedig aránylag könnyen belátható ennek a hozzáállásnak ("utána volt, tehát miatta volt") az abszurditása. Mondok egy kevésbé drámai példát: a listán szerepel a súlygyarapodás. Namármost, valószínűleg mindenki egyetért, hogy ez az esemény hébe-hóba, de előfordul az emberrel akkor is, ha éppen nem kapott HPV-oltást. Kérdés ennek a valószínűsége, igen szolidan ez mondjuk legyen 1 ezrelék / fő / hó. (Tehát minden embernek minden hónapban 1 ezrelék valószínűséggel fog a súlya – általa már nemkívánatosnak minősített módon – gyarapodni.) Hangsúlyozom, ez a súlygyarapodás kockázata HPV-oltás nélkül; az ún. baseline rizikó vagy háttérráta, tehát az esemény "magától" (beavatkozás nélkül) történő bekövetkezésének valószínűsége. Igen ám, de ez másként megfogalmazva azt jelenti, hogy ha veszek 1000 embert, akkor köztük 1 hónap múlva várhatóan 1-et találni fogok, akinek nőtt a súlya – mindenféle HPV-oltás nélkül. Tízezer ember között ez már 10. Ha viszont én most ezt a tízezer embert beoltom a HPV-vakcinával, akkor természetesen nem tudom megmondani (időgép hiányában), hogy hánynak gyarapodott volna a súlya oltás nélkül az oltás követő 1 hónapon belül… de azt meg tudom mondani, hogy várhatóan 10-nek. Ha tehát az oltást követő hónapban (megint csaljunk a védőoltás-ellenesek javára, és szabjuk meg ilyen szűken az intervallumot) 10 bejelentés érkezik súlygyarapodásról, akkor az tökéletesen megfelel annak a helyzetnek, hogy az oltásnak nincs hatása a súlygyarapodás rizikójára. Talán már mindenki érti a fonákságot, amit a védőoltás-ellenesek kihasználnak: ha mondjuk ez a szám ténylegesen 5 a 10 helyett, akkor lehet turnéztatni a tévében 5 embert, hogy ők bezzeg az oltás hatására így jártak – miközben ez a helyzet, ha jobban megnézzük, a valóságban azt jelenti, hogy az oltás véd a súlygyarapodás ellen! Hiszen a várható 10 helyett csak 5 ilyen eset volt. De ezzel a mai médiában nagyon nehéz harcolni, hiszen ha egy oltásból sokat adnak be (az ominózus HPV-oltásból a világon már több mint 100 milliót!), akkor bármilyen marginális valószínűségű eseményből tekintélyes számú alany lesz még akkor is, ha a valóságban nincs többletrizikó (tehát csak "véletlen egybeesések" történtek, a szónak a fenti értelmében). Ez az, amik sokak számára – egyénileg szerintem teljesen érthető módon – nehezen emészthető: "itt van a beteg gyerekem, úgyhogy ne gyere nekem ezzel a véletlen egybeeséssel, mégis mennyi ennek a valószínűsége?!". És csakugyan, az ilyen véletlen egybeesés (tehát a háttérrátába tartozó esemény előfordulása épp az oltás után) lehet igen valószínűtlen is, pláne ha a betegség általában is ritka, vagy ha nagyon szoros az időbeli egybeesés – épp ezért mondtam, hogy a logika érthető. A probléma, amit ez az okfejtés figyelmen kívül hagy, hogy viszont nagyon sok oltást is adunk be, márpedig nagyon sok megfigyelésből nagyon kis valószínűségű esemény is elő fog fordulni. Ha ezt valaki nem hajlandó elfogadni, az olyan, mintha azt mondaná, hogy nem hiszi el, hogy a lottóötöst megnyerte valaki, hiszen ennek igen kicsi az esélye (pedig ennek aztán tényleg nagyon kicsi, kevesebb mint 1 per 40 millió!). Valóban, az, hogy én megnyerem a lottóötöst tényleg nagyon valószínűtlen, de hogy valaki megnyeri, már egyáltalán nem az! – épp azért, mert nagyon sokan lottóznak. És csakugyan, rendszeresen el is viszik a főnyereményt, a győztes pedig joggal mondhatná, hogy "itt van ez a rengeteg pénz, úgyhogy ne gyere nekem ezzel a véletlenséggel, mégis mennyi ennek a valószínűsége?!"...
Ez lehetőséget ad turnézni a tévéstúdiókban akkor is, ha a védőoltás a valóságban nem növeli, vagy – extrém esetben – akár kimondottan csökkenti a szóban forgó esemény kockázatát. Ki fog ugyanis utánaszámolni a fentieknek az átlag tévénézők közül…? Holott jól látható, visszatérve az előbbi példára, hogy amíg a védőoltás-ellenesek nem tudnak minden ezer oltott után 1 súlygyarapodást felmutatni (egyetlen hónapon belül, természetesen, ha nagyobb intervallumot nézünk, akkor még többet!), addig a védőoltás nem növelte ennek a rizikóját! Csak hát ezt nehéz a mai média viszonyai mellett bemutatni: enyhén szólva is hatásosabb a stúdióban tíz, gyermeke – például – rákja miatt sírdogáló szülő, mint egy olyan megjegyzés, hogy már elnézést, de amíg nem találnak húszat, addig az oltás pont hogy csökkentette a rák kockázatát… Kellően sok oltás után még a ritka eseményekből is bőven lesz "oltáskárosodott" gyerek – a háttérnek meg ugyan ki fog utánagondolni. (Most arról nem is beszélve, hogy a VAERS egy passzív jelentőrendszer, így a bejelentett események gyakorisága – mivel ismeretlen nagyságú háttérpopulációból származnak – meg sem határozható.) A dolognak egyébként az a gyomorforgató része etikai szempontból, hogy míg nekem, értelemszerűen, eszembe sem jutna, hogy ezeket a tragédiákat mondjuk kisebbítsem (magától értetődő, hogy például egy gyermekrák leírhatatlan tragédia a családnak, akármi (!) is okozta), addig a védőoltás-ellenesek egy része láthatóan tizedmásodpercnyi gondolkodás nélkül csinál az ilyen esetekből cirkuszi látványosságot (elsősorban épp a tragédiát átélteket megalázva!), csak azért, hogy kihasználják ezt önös céljaikra.
A fenti számok, 1 ezrelékkel meg 10 beteggel nyilván csak illusztratívak voltak, de meg lehet ezeket, tehát a háttérrátát, valódi adatok alapján, pontosan is határozni. Az oltásbiztonságról szóló részben mutatom be részletesebben ennek a módszerét, a lényeg most a végeredmény, egy példát említve: hogy 1 millió oltás beadása után 4,94 esetben várható 1-es típusú cukorbeteg fellépése az oltás beadását követő egy héten belül ha az oltás és a betegség között nincs összefüggés. Ennyi a véletlen egybeesések száma, ilyen értelemben; és ez a 4,94 már nem illusztratív szám, hanem egy adott ország adatai alapján kiszámolt pontos érték. Ha ennél több fordul elő, akkor felmerül, hogy az oltás okozza a betegséget, ha ennél kevesebb, akkor felmerül, hogy az oltás véd ellene – miközben még így is van kit mutogatni a weboldalon (és nem hazugság!), mint aki az oltás beadása után egy héten belül cukorbeteg lett, ugyan már, senki ne magyarázza, hogy itt nincs összefüggés...
Zárásként hadd mutassak még egy, meglehetősen látványos demonstrációt a háttérráta problematikájára. A következő ábrát az oltásbiztonságról szóló részben fogom részletesen ismertetni, most elég róla annyit tudni, hogy egy bizonyos betegség előfordulását mutatja (a piros vonallal egyelőre ne törődjünk) az év egyes heteiben egy nagyvárosban. A 33. és 34. hetén a város gyermekeit beoltották egy vakcinával, jó részüket ráadásul egyetlen napon, az ábrán külön is megjelölt augusztus 16-án.
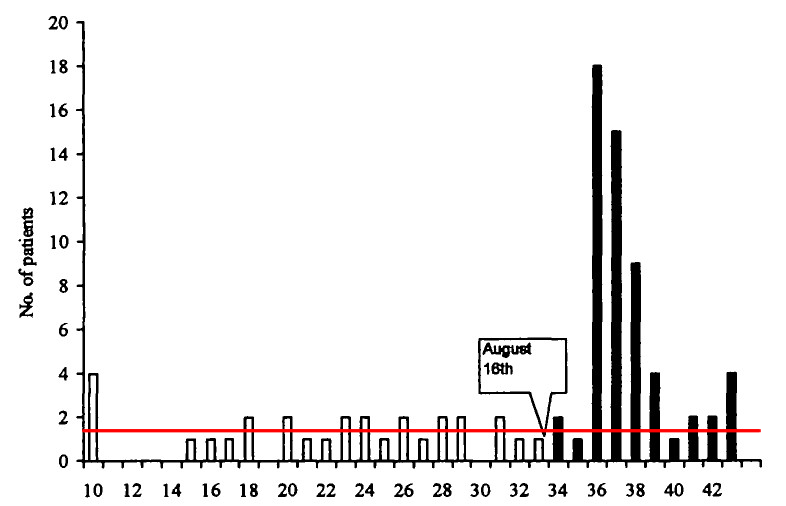
Az ábra erős bizonyíték amellett, hogy az oltás tényleg okozza a betegséget, de most nem is ez az igazán fontos. Ha megnézzük az oltás beadása előtti, az ábrán fehér oszlopokkal jelölt adatokat, akkor azt látjuk, hogy a betegség abban az időszakban, tehát az oltás hiányában is előfordult – ez tehát nem más, mint a háttérráta. Hogy jobban látható legyen, piros vonallal be is jelöltem. Igen ám, de gondoljuk csak végig: ez azt jelenti, hogy miközben ez az oltás nagyon is okozta a betegséget, miközben nem is kevés eset fordult elő, még a következő heti (!) betegáradatban is volt, aki nem az oltástól betegedett meg! (Ugyebár aki a piros vonal alatt van!) Amit valószínűleg – és ezt meg is értem – nem lenne könnyű elmagyarázni az érintettek szüleinek, pedig az ábra félreérthetetlenül mutatja mi a helyzet.
Megfordítva, ha az oltásnak semmilyen köze nem lenne a betegséghez, akkor a fekete oszlopok is ugyanúgy a piros vonal körül ingadoznának. A piros vonal körül, nem a nullában! Újra visszaérünk ugyanoda: ebben az esetben is lenne megbetegedés, akár közvetlenül az oltás után is, pedig az oltásnak köze nem volt a betegséghez – és ez most biztos, hiszen láttuk a helyzetet abból az időszakból, amikor még csak be sem adták az oltást. De tényleg ugyanoda érünk vissza: mennyi esély van elmagyarázni egy ilyen ábrát, és a mögötte lévő megfontolásokat, amikor a másik oldalon az oltás után kórházba került gyerekek képeit mutogatják...
Visszatérve az alapkérdésre, a korábbi okfejtés azért volt különösen egyértelmű, mert az mindenféle mélyebb megfontolás nélkül, bárki számára érzékelhető, hogy a "súlygyarapodás" egyáltalán nem olyan ritka esemény, így elég könnyen érezhető, hogy mi a különbség az "után" és a "következtében" között. Nem kell azonban magyaráznom, hogy ez milyen hatásos taktika a súlygyarapodásnál drámaibb esetekben, ahol ráadásul ez a különbség sem olyan egyértelmű. Erre szolgál részletesebb példával a következő eset.
Egy konkrét (és tipikus…) példa
Nemrég olvastam egy védőoltás-ellenes honlapon, hogy a gyártó cég "kiszivárgott" "bizalmas" dokumentumai szerint a vizsgált kétéves periódusban 36 csecsemő halt meg röviddel az Infanrix hexa nevű védőoltás beadását követően. Irgalom atyja ne hagyj el! Micsoda elképesztő tömeggyilkosság! – mondhatja az egyszeri olvasó; mi azonban gondolkozzunk egy kicsit.
(Az egész hír egyébként David Icke weboldalán jelent meg, aki szerint a Földet emberi formát öltött alakváltó hüllők irányítják – nem viccelek! aki nem hiszi nézze meg az illető weboldalát! –; a cikk szerzője Christina England, aki abban utazik többek között, hogy saját gyermeküket megölő szülőket próbál felmentetni arra hivatkozva, hogy a gyermek sérüléseit vakcinák okozták (!), és nem a bántalmazás. Sajnos ez sem vicc. Láthatjuk tehát, hogy morálisan és intellektuálisan is rendkívül kifinomult társasággal van dolgunk, de legalább mi tartsuk magunkat a korrekt vitamódszerekhez, és ne genetikusan érveljünk, hanem nézzük magát az állítást.)
Az első kérdés, hogy egyáltalán hiteles-e ez a hír. Ezt nem álltam neki tételesen ellenőrizni, elfogadom, hogy az – annál is inkább, mert mint majd hamarosan látni fogjuk, ezek a számok nem aggodalomra adnak okot, hanem épp ellenkezőleg, kimondottan megnyugtatóak.
(Természetesen már itt, tehát a hír forrásának megadásánál is jön a szokásos összeesküvés-elmélet mánia, illetve a modern médiához passzoló, ezt sajnos jól csinálják, bombasztikus címadás: "bizalmas" "kiszivárgott" dokumentumok, hű. No hát, elárulom, hogy a szupertitkos kiszivárgott dokumentum nem más, mint az Infanrix ún. PSUR-ja (Periodic Safety Update Report, nagyjából időszakos biztonsági felülvizsgálati jelentés) amelyet minden centralizáltan törzskönyvezett gyógyszerre hat havonta el kell készítenie a gyártónak, és be kell küldenie az európai gyógyszerhatóságnak. A PSUR-nak tartalmaznia kell a vizsgált időszakban történt, gyógyszerbiztonságilag releváns fejleményeket, részletes értékeléssel, szükség esetén intézkedési javaslattal és így tovább. Egyébként ezeket az Infanrix-es PSUR-okat feltétlenül érdemes mindenkinek megnéznie! Több mint 1200 oldalnyi (!) hihetetlen részletességű dokumentálása minden jelentett nemkívánatos eseménynek, rengeteg statisztika, kiértékelés, "nyomozások" a felmerült gyanús halmozódások vonatkozásában… Úgyhogy én személy szerint nagyon örülök annak, hogy ez a szupertitkos dokumentum "kiszivárgott", így a jövőben lesz hová irányítani a védőoltás-elleneseket, amikor azzal jönnek, hogy a mellékhatásokkal a kutya sem törődik, a gyártók letagadják a hatóság előtt, stb.)
Szóval, ott tartunk, hogy két év alatt 36 gyermek meghalt röviddel a védőoltás beadását követően. Gyanús ez? A dolog ott kezdődik, hogy a cikk szerzője szerint azért az, mert eszerint minden hónapra másfél halálozás jut. Erre már nehéz mit mondani: eszerint akkor a kockázat nem attól függ, hogy hány beadott vakcinára jutott 36 halálozás, hanem attól, hogy azokat mennyi idő alatt adták be? Akkor a szerző szerint ha ugyanezeket az oltásokat tizedannyi idő alatt adnának be, akkor tízszer rosszabb lenne a vakcina statisztikája? (Ha meg 100 év alatt, akkor szinte tökéletessé válna?) Nem semmi…
Tehát – természetesen… – ezt a számot a beadott vakcinák számához kell viszonyítani. A dokumentum ezt is pontosan tartalmazza: az utolsó PSUR időpontjáig (azaz 2000. október 23. és 2011. október 22. között) összesen 72 931 338 dózist adtak el. Ebben az időszakban a jelentett halálozások száma 74 volt, ami más szóval azt jelenti, hogy a halálozás kockázata jó közelítéssel 0,1 per 100 ezer oltás. (Még más szóval, kb. minden 1 milliomodik oltásra jutott egy halálozás. Az összehasonlítás kedvéért, nemzetközi felmérések szerint nagyjából ugyanekkora halálozási kockázata van 15 km kerékpározásnak, vagy fél liter bor megivásának…)
Így máris máshogy hangzik a dolog, de a kutya valójában nem is itt van elásva! Én ugyanis nem egyszerűen azt akarom állítani, hogy ez a kockázat kicsi – erre még mindig lehetne, bár az előzőek fényében félig-meddig manipulatív módon, azt mondani, hogy azt az egy szülőt ez nem vigasztalja. Itt azonban többről van szó, és aki végigolvasta az eddigieket, az minden bizonnyal sejti is, hogy mi fog következni. Ez a számítás ugyanis még mindig nem korrekt, hiszen azzal, hogy egyszerűen ráosztottuk a halálozások számát a beadott oltások számára, azt mondtuk, hogy kivétel nélkül minden halálozást a vakcina okozott – ezt talán még a legelszántabb védőoltás-ellenes sem gondolja komolyan, már pusztán azért sem, mert csecsemők halnak meg Infanrix hexa oltás nélkül is. (Megint csak: a halálozásnak van egy háttérkockázata.) Ezeket a halálozásokat nyilván nem számíthatjuk bele az oltás kockázatába: minket nem a kockázat, hanem az oltás miatti többletkockázat, az ún. oltásnak tulajdonítható kockázat (angol irodalomban: attributable risk) érdekel. Az ezt figyelembe nem vevő számítás az emberek manipulálására ugyan kitűnő (36 vagy épp 74 csecsemőhalál, ennél aligha kell drámaibb!), de a valósághoz nem sok köze van.
A kérdés már csak az, hogy mégis, hogyan tudjuk elkülöníteni az esetleges vakcina következtében fellépő halálozásokat a vakcina után fellépő halálozásoktól. (Kiegészítésként teszem hozzá, hogy most kizárólag az epidemiológiai adatok oldaláról közelítek, azzal nem is foglalkozom, hogy mechanizmusát tekintve mennyire hihető egy adott halálozásról, hogy köze volt az oltáshoz – pedig ez adott esetben nagyon nem mindegy: ha a gyermeket a védőoltás beadása utáni napon elgázolja egy autó, akkor van okunk feltételezni, hogy ez csak az oltás után, de nem annak következtében történt. (Bár elnézve egyes védőoltás-elleneseket, ennek nyilvánvalóságában sem vagyok teljesen biztos…) Én most azonban ezzel nem foglalkozom, minden egyes jelentett halálozást, akár még ezt is, ha volt ilyen potenciálisan a védőoltás által okozottnak veszek, azaz: nem vizsgálom a biológiai plauzibilitását annak, hogy az oltás egyáltalán halált tud-e okozni.) A megoldás kézenfekvő: próbáljuk meghatározni ezt a háttérrátát!
Jelenleg a csecsemőhalandóságban a világ élvonalába tartozó országok 2-4 per 1000 élveszületés halandóságnál tartanak, újszülöttkori halandóságban (28 nap alatti halálozási ráta) pedig 0,5-3 per 1000 körül. Számoljunk tehát 3 per 1000 csecsemőhalandósággal, és 2 per 1000 újszülöttkori halandósággal – ez nagyjából ma a világon a legjobb amit el lehet érni, így jó összehasonlítási alap lesz, nem érhet az a vád, hogy szándékosan magas értéket választottam... Összevetve a kettőt, azt kapjuk, hogy annak a kockázata, hogy egy élve született csecsemő 1 hónapos és 1 éves kora között meghal, nagyjából 1/1000. (Azért ezt a korosztályt választottam, mert az Infanrix hexa-k túlnyomó többségének a beadására ebben az intervallumban kerül sor szinte minden országban. Azért lehet csak ilyen óvatosan fogalmazni, mert az egyes országok immunizációs tervei, így a beadott oltások darabszáma és ütemezése eltérhet egymástól.) Ez más szóval azt jelenti, hogy közelítésünk szerint Infanrix hexa nélkül egy csecsemő minden egyes nap \( \left(1/1000\right) / \left(365-28\right)=2,\!97\cdot 10^{-6}\) valószínűséggel hal meg 1 hónapos és 1 éves kora között. (Az egyszerűség kedvéért feltételeztem, hogy ezen az intervallumon belül konstans rátájú a halálozás.) És ne felejtsük el, hogy ez a közelítés igencsak kedvez a védőoltás-elleneseknek, hiszen a csecsemőhalandóság elkerülésében világélvonalban lévő országok átlagát vettem a számításhoz alapul.
Ez valóban roppant kicsi szám, és első ránézésre a védőoltás-elleneseket erősíti meg: ha az oltás beadása utáni napon meghal egy gyermek, az tényleg rendkívül kis valószínűségű esemény, úgyhogy joggal lehet "gyanús". Mi ebben a mondatban a hiba? Az, hogy kimaradt egy szó: ha az oltás beadása utáni napon meghal egy gyermek, az önmagában tényleg rendkívül kis valószínűségű esemény. Valóban, ha 1 oltást adunk be, akkor a halálozások várható száma \(2,\!97\cdot 10^{-6}\), ha ehhez képest 1 lesz, az felettébb gyanús. Igen ám, de ha 2 oltást adunk be, akkor a halálozások várható száma máris \(2\cdot2,\!97\cdot 10^{-6}\), ha 10-et akkor \(2\cdot2,\!97\cdot 10^{-5}\) és így tovább. És ezen a ponton emlékezzünk vissza arra, hogy az Infanrix hexa-ból több mint 70 milliót (!) adtak el! Ez tehát azt jelenti, hogy a beadás utáni napon várható halálozások száma annak feltételezése mellett, hogy az oltásnak semmilyen hatása nincs a halálozásra \(70\cdot 10^{6} \cdot 2,\!97 \cdot 10^{-6}=207,\!7\)! Tehát ha a védőoltás-ellenes oldalon lobogtatott papíron szereplő összes halálozás kivétel nélkül az oltás beadását követő egy napon belül történt volna, még akkor is elmondható, hogy a 74 halálozás nem hogy több, hanem épp ellenkezőleg: kevesebb annál, mint amit akkor várnánk, ha az oltásnak semmilyen hatása nem volna a halálozásra! Ha az oltás valóban növelné a halálozást, akkor az ott kezdődne, hogy nem 74, hanem több mint 208 esetet kellett volna látnunk… a legelső napon! Ha az oltást követő második napi halálozásokat is számoljuk, akkor a gyanú felvetéséhez szükséges halálozások száma 416, ha egy egész hét a gyanús periódus akkor 1456 és így tovább. Természetesen itt be kell kalkulálnunk az esetleges "underreporting"-ot (azaz, hogy nem minden esetet jelentenek), de egyrészt egy olyan drasztikus eseményre, mint az oltást követő napon történő halálozás, ez vélhetően csekély, másrészt látszik, hogy még ezzel együtt is többszörös a különbség, úgyhogy ennek – és persze a szokásos mintavételi ingadozásnak, hiszen itt egy mintáról van szó – bőven van hely. És ismétlem: mindezt a gyermekhalandóságban világélvonalbeli országok adataihoz viszonyítva. (Másként megfogalmazva ugyanezt: az adatok szerint az Infanrix hexa oltást követő nap halálozási kockázata – minden országból összevonva! – még a világ ilyen szempontból vezető országainak szintjét sem éri el.)
Természetesen a fentiekből magukat a numerikus végeredményeket nem szabad túl komolyan venni, ezért nem is akarom kijelenteni, hogy az oltás látványosan csökkenti a halálozás kockázatát, de az alapvető helyzetet jól mutatja (és nem akartam technikai részletekkel bonyolítani a gondolatmenetet).
Összefoglalva: ezek az adatok nem ijesztőek, hanem kimondottan megnyugtatóak!
Két dolog látható ebből. Az egyik, hogy a fenti számolás jól láthatóan a temporális asszociáció szorosságát is figyelembe vette, magyarán arra sem hivatkozhatnak a védőoltás-ellenesek, hogy "de hát ez egy napon belül történt!". Másrészt látszik, hogy a baseline kockázat maga valóban nagyon kicsi… viszont rengeteg oltást is adtak be. (Egy kicsit visszajutottunk oda, amit az elején mondtam: ha nem 207, csak 206 haláleset van, az azt jelenti, hogy az oltás nemhogy bajt nem okoz, hanem épp ellenkezőleg, véd a halálozás ellen – de mégis, ki az, aki ilyenekre gondolna, ha a tévében egymás után látna 206 (!) síró anyukát, akik elmesélnék, hogyan halt meg az oltás másnapján a kicsi csecsemőjük… ezért is mondtam, hogy ezzel nehéz felvenni a versenyt.)
Egy még konkrétabb példa
Most egy az előzőhöz rendkívül hasonló példát szeretnék mutatni, csak még "közelebbről" megvizsgálva.
Ott venném fel újra a fonalat, hogy gyerekek halnak meg védőoltásoktól függetlenül is, tehát a védőoltások veszélyességére nem következtethetünk önmagában abból a tényből, hogy egy gyerek a védőoltás után valahány nappal meghalt. Viszont ezen a nyomvonalon kicsit tovább is mehetünk, és tehetünk más érdekes észrevételeket is. Az eset, amit most közelebbről meg fogok vizsgálni, arról szól, hogy egy másfél éves belga gyermek meghalt az MMR oltása után. Az erről beszámoló védőoltás-ellenes oldal minden szükséges eszközt felvonultat: drámai cím (nem "meghalt az MMR-oltás után" vagy ilyesmi, még csak nem is "meghalt a következtében", nem, dehogy: "az MMR oltás gyermeket ölt [!]", így), fénykép a gyerekről, hogy mindenki közel érezze magához a tragédiáját stb.
Vizsgáljuk azonban meg közelebbről a történetet! Az igazán érdekes ugyanis, hogy a szerzője semmilyen orvosi kapcsolatot nem állított fel az oltás és a halálozás között, egész konkrétan egyetlen szót nem vesztegetett arra, hogy pontosan miért "állt meg a szíve" az oltás után. Az egyetlen és kizárólagos ok, amire az oltás meggyanúsítását alapozta (és ebben persze nem fogta vissza magát...), az az időbeli közelség. Hát akkor piszkáljuk meg ezt egy kicsit!
A konkrét esetben 9 nappal az oltás után következett be a tragédia. Azt fogjuk megvizsgálni, hogy valóban "gyanús" egybeesésnek minősül-e a 9 nap múlva történő halálozás. Vajon jogos ez alapján olyanokat írni, hogy az oltás "ölte meg" a gyereket...?
A módszerünk nagyon egyszerű lesz: kiszámoljuk, hogy azon feltételezés mellett, hogy az MMR és a halálozás között nincs összefüggés, mekkora a valószínűsége annak, hogy valaki az oltástól számított 9 napon belül meghal. Nyilván nem nulla, ez a kulcsgondolat, hiszen ha van egyáltalán halálozás 12 hónapos kor környékén, márpedig van, akkor az a puszta vakvéletlennek köszönhetően is bekövetkezhet a 9 napos időablakon belül. Ha ez a valószínűség nagyon alacsony, akkor valóban elgondolkodtató az eset, ha nem, akkor nincs okunk feltételezni, hogy a fenti esemény a véletlen egybeesésen túl máson is múlt volna. Hangsúlyozom, hogy a következőkben nem nyilatkozom arról, hogy hihető-e az ilyen összefüggés – egyszerűen kiszámolom, hogy ha nincs ilyen összefüggés, akkor mi várható (ha-akkor!); hiszen ha ez egybeesik a konkrét eset adataival, akkor nincs okunk összefüggést feltételezni.
Belgiumban az MMR-t 12 hónapos korban adják. Annak a valószínűsége, hogy egy olyan gyermek esetében, aki 1 és 2 éves kora között hal meg, ez a halálozás teljesen véletlenül az oltást követő 9 napon belülre esik, nyilván 9 / 365 = 0,0247. (Hiszen ha függetlenek egymástól, akkor a halálozás nem "sűrűsödik" az oltás beadását követő 9 napban bármely más 9 naphoz képest. Ha viszont az oltásnak valóban van ilyen hatása, akkor nagyobb ez a valószínűség.) Az egyszerűség kedvéért itt is azt feltételeztem, hogy 1 és 2 éves kor között a halálozás intenzitása állandó, amivel történetesen az oltás ellen csalok, a valóságban ugyanis ez csökkenő tendenciájú, így természetes és várt, hogy 1 éves kor környékén, beleértve az 1 év és 1 év plusz 9 nap közti ablakot is, több halálozás van, mint más 9 napokban.
Belgium legfrissebb hivatalos mortalitási táblázatából látható, hogy 1 és 2 éves életkor között 37 halálozás van évente. Ez azt jelenti, hogy a teljesen véletlen egybeesések várható száma \(0,0247 \cdot 37 = 0,\!91\). (Annak a valószínűsége, hogy egyetlen ilyen egybeesés sincs, nyilván \(\left(1-0,\!0247\right)^{37} = 0,\!397\). Annak a valószínűsége, hogy 1 egybeesés van, tehát, hogy az oltás utáni 9 napon belül egy haláleset következik be mindenféle összefüggés nélkül: \(37 \cdot 0,\!0247 \cdot \left(1-0,\!0247\right)^{36} = 0,\!371\); annak, hogy 2: \(\left(37\cdot36/2\right) \cdot 0,\!0247^{2} \cdot \left(1-0,\!0247\right)^{35} = 0,\!169\) és így tovább.)
Összefoglalva: ha az oltás nem növeli a halálozás valószínűségét, akkor évi átlag 0,91 esetben várhatjuk, hogy az oltás beadását követően (9 napon belül), de attól teljesen függetlenül, puszta véletlen egybeesésből, meghal egy gyerek. Ha az oltásnak van halálozási valószínűséget növelő hatása, akkor ez a szám nagyobb. Annak az esélye, hogy egyetlen ilyen eset sincs egy évben, 40%, annak, hogy 1 vagy annál több van, 60%, ha feltesszük, hogy az oltás nincs semmilyen hatással a halálozásra.
Következésképp évi 1 ilyen eset tökéletesen megfelel annak, amit akkor várhatunk, ha az oltások és a halálozás között semmilyen összefüggés nincs.
Ezt a példát azért szeretem egyébként különösen, mert jól mutatja, hogy miért fontos a kritikus gondolkodásmód, egyszerűbben megfogalmazva: hogy végiggondoljuk, amit olvasunk. Amikor először láttam ezt a cikket, elgondolkodtam, utánanéztem és a fentire jutottam. Ami a legfontosabb, hogy ehhez semmilyen szupertitkos eszköz nem kellett: Google, negyedóra-félóra és egy kis józan ész. Ennek ellenére büszke voltam, hogy ez eszembe jutott, főként azért, mert láthatóan senki más nem gondolkozott el a többi olvasó közül ilyeneken – mindenki átkozta az MMR-t. Pontosan ahogy a védőoltás-ellenesek azt meg is tervezték...
Utóirat: az ominózus védőoltás-ellenes oldalról a fenti szövegű hozzászólásomat fél órán belül kimoderálták. Hiszen mint tudjuk, a védőoltás-ellenesek a nyílt vita hívei...
Záró gondolatok (az anekdotikus bizonyítékokról)
Számtalanszor utaltam már rá a korábbiakban is, hogy az ezzel a kérdéskörrel kapcsolatos problémák nem is igazán tudományosak, sokkal inkább pszichológiaiak.
Az oltás után meghaló, megbetegedő gyermekek történeteinek a médiában történő megjelenése szükségképp egy torzított kép: akinek a gyerekével a világon semmi nem történt az oltás után, nem fog betelefonálni a rádióműsorba vagy weboldalon hozzászólni, hogy ezt elmondja, mindenesetre sokkal kevésbé, mint akinek baja lett. Így aztán aki a média hírei alapján próbálja ezt megbecsülni, egy egészen eltorzított arányt fog látni, hiszen olyan hírt nem fog olvasni a címlapon, hogy "Pistikével semmi különös nem történt az oltás után", de az, hogy "Pistike (2) az intenzív osztályon az oltása után! Megrázó képek!" nagyon is címlapra esélyes. Ezért az előbbi esetekről szinte soha nem kap hírt, az utóbbiakról ellenben sokkal inkább.
Márpedig, mint azt remélem az előbbiekben sikerült kellően alátámasztanom, az arányok jelentik a kérdést. A kérdés nem az, hogy van-e aki oltás után lesz beteg (nyilván igen), hanem az, hogy több van-e, mint anélkül lenne. Példát tehát mindig lehet hozni ilyenre, és pontosan emiatt nem megyünk sokra ezekkel az egyedi példákkal. Ez az anekdotikus bizonyítékok igazi problémája: nem is elsősorban az, amit az anekdota szó sugall, hogy ti. igaz-e egyáltalán, persze, sokszor az is kérdés, de a legnagyobb gond, hogy – még ha igaz is – nem tudunk ez alapján arányt számolni. Ahhoz ismernünk kellene az összes esetet, mégpedig minden kimenetre vonatkozóan – csakhogy az anekdoták (nagyon) nem ugyanolyan arányban terjednek el az egyes kimenetek esetén...
Az, hogy valaki – például – autista lett egy oltás után, egyénileg természetesen megrendítő dráma és én mélységesen együtt is érzek a családdal, de ez epidemiológiailag nem sokat jelent. A konkrét családnak ez persze valószínűleg édesmindegy, de a népegészségügynek nem az. Ha azt kérdezik, hogy én személy szerint együttérzek-e egy ilyen családdal, akkor a válaszom természetesen az, hogy maximálisan (mint ahogy valószínűleg minden ember ugyanezt válaszolná, hiszen az együttérzés nem annak szól, hogy oltástól, genetikától, valamilyen még ismeretlen toxintól vagy épp a csillagok szerencsétlen állásától lett autista a gyerek), de mint az oltás biztonságossága kapcsán felhozott érv, nem tudom elfogadni. Ugyanúgy, mint ahogy azt sem tekintem érvnek ellentétes előjellel, hogy én meg nem lettem autista! Erről ugyanis nem lehet "személyes tapasztalatok", egyes példák alapján dönteni. Aki tehát gyerekeket mutogat azzal, hogy íme ők is egy oltás után lettek autisták (/haltak meg /stb.), az valójában nem érvel, hanem egyszerűen manipulálni akar – ez ugyanis nem érv, csak akkor lenne az, ha valaki azt állította volna, hogy az oltottak között nincs autista... csakhogy ilyet senki nem mondott. Az ilyen ember tehát valójában nem a mutogatott betegek érdekeit szolgálja, épp ellenkezőleg: gátlástalanul kihasználja tragédiájukat egyéni céljai elérésére (amelyek, nem mellesleg, végeredményben éppen ahhoz vezetnének, hogy még több beteg legyen).
Végül megjegyzem, hogy a fentiek szerintem olyannyira nyilvánvalóak, hogy ezeket valószínűleg a védőoltás-ellenesek is tudják, és egész más miatt ragaszkodnak mégis az ilyen példák perverz részletességű, fényképekkel illusztrált alapos bemutatásához. Pontosan tudják, hogy az emberek érzékenyek a gyermekhalálokra és súlyos betegségekre, ha pedig ezt megfelelő körítéssel tálalják (könnyeikkel küszködő szülők a YouTube-videón, kép a gyerekről, amint vidáman játszik a nagy piros labdával, majd kép a gyerekről, amint csövek lógnak ki belőle az intenzív osztályon, utána kép a temetésről fekete keretben stb., stb.), akkor olyan érzelmeket tudnak felkorbácsolni az olvasókban, hogy azokat – immár a racionalitás teljes kikapcsolása után – szinte bármi ellen tudják fordítani. Például a védőoltások ellen. Nem kell sok: pár mondatban felvázolni, hogy ez egy héttel egy oltás megkapása után történt, és kész is. Ez egy gyomorforgató, primitív – de sajnos nagyon is hatásos – manipuláció, ami azért különösen visszataszító számomra, mert ilyenkor a védőoltás-ellenesek (teljesen tudatosan) a gyermek fájdalmát, egy család fájdalmát nem enyhíteni akarják, hanem egész egyszerűen csatasorba állítják céljaik elérésére.
Szóval: gyomorforgató, primitív manipuláció, de sajnos működik. Ráadásul nagyon nehéz ellene védekezni, hiszen arról nem lehet látványos anyagokat összerakni, hogy Pisti megkapta az oltást, aztán egy hét múlva... nem történt semmi. Arról könnyű látványos videót készíteni, hogy Pisti hogyan halt meg valamiben, arról már jóval nehezebb, hogy hogyan nem halt meg valamiben (mondjuk kanyaróban).
(A dolog annál is inkább felháborító, mert ha valaki esetleg elpisszenti magát, hogy kanyaróban is halnak meg emberek, még napjainkban is, akkor persze abban a tizedmásodpercben a nyakába kapja a védőoltás-ellenesektől, hogy ne riogasson ilyen halálesetekkel, micsoda túlkapás ilyen ritkaságokat kiragadni, felháborító...)
Tehát bár nehéz ez ellen védekezni, de hiszek abban, hogy nem lehetetlen. Ismeretterjesztéssel, felvilágosítással el lehet érni, hogy minél kevesebb embert tudjanak félrevezetni. Az igazság terjesztése sajnos szerintem ugyan hátrányban van a valótlanságok terjesztésével szemben, de hiszek abban, hogy hosszú távon az igazságnak kell felülkerekednie.

