A bejegyzés I. része itt olvasható.
A dolog nem csak a SIRV-modell sajátja, ami miatt esetleg azt gondolhatnánk, hogy csak egy erre a modellre jellemző modellezési furcsaság. A korábban említett sokkal komplexebb modellben is ugyanúgy megjelenik ez a mézeshetek jelenség (lásd a következő ábrát, itt az effektus nem az éppen rossz átoltottság, hanem az éppen rossz szekunder hatásosság példáján van szemléltetve). Sőt, egészen meghökkentő módon itt több mint 50 év (!) elteltével robban ki a járvány, ennyi idő telik el, jórészt a tényleges felszámolástól megkülönböztethetetlen körülmények között, mígnem, látszólag "a semmiből", előtör a betegség. Ez a példa is arra figyelmeztet, hogy csak azért, mert egy betegség régóta nem fordult elő, akár szó szerint semennyire, még nem lehetünk benne biztosak, hogy meg is szabadultunk tőle – rossz esetben kitörhet a járvány szinte minden előzmény nélkül is. Erre mindig gondolnunk kell népegészségügyi szinten. Természetesen ez nem jelenti azt, hogy teljesen eszköztelenek vagyunk ezzel szemben: rendelkezésre állnak immunológiai eszközök egy alany fogékonyságának a felmérésére, márpedig ha ilyeneket elég sok, lehetőleg véletlenszerűen kiválasztott emberen alkalmazunk, akkor jó képet tudunk kapni arról is, hogy a fogékonyak aránya hogyan alakul a lakosságon belül – szemben a szokásos járványügyi információgyűjtéssel, ami csak a megbetegedettekről szolgáltat információkat, ami a fentiek miatt kevés lehet. A fogékonyakra vonatkozó információ azonban mutatja e csoport létszámának esetleges halmozódását, és így előrejelezheti az ilyen járványt is, emiatt alkalmazása mindenképp kívánatos lenne.
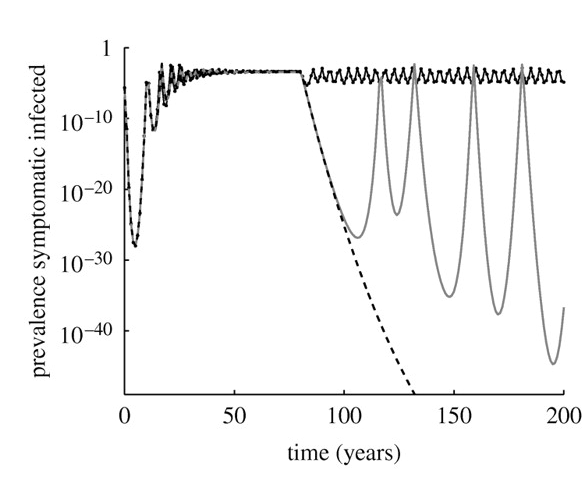
A vakcinációs "mézeshetek" ("honeymoon") effektus a korábbi ábrán már látott komplex modell esetében (az oltási program a 80. évben indul, az előtte látott szakasz a modell beállása az oltás nélküli egyensúlyra), a függőleges tengelyen a betegség előfordulásával, logaritmikus skálán; itt az átoltottság állandó, ám a védőoltás szekunder hatásossága eltérő – szaggatott vonal: nincs gyengülés (betegség felszámolása), pontozott vonal: 30 év elteltével bekövetkező gyengülés (túl rossz vakcina, felszámolás fel sem merül), halványabb szürke vonal: 80 év elteltével bekövetkező gyengülés (rossz, de csak éppenhogy rossz vakcina: mézeshetek effektus)
Ami az egészben a fantasztikus, hogy ilyen és ehhez hasonló modellekkel ezt a jelenséget már az előtt megjósolták, mielőtt bekövetkezett volna: a kutatók az 1980-as években rámutattak, hogy vannak olyan országok, tipikusan a fejlődő világban, ahol a paraméterek pont olyanok, hogy ez bekövetkezhet; előre megmondták, hogy hol állnak fenn ezek a feltételek, mikor fordulhat ilyen elő – majd ahogy megjósolták, be is következtek ezek a járványok!
Amit nagyon fontos látni, hogy ez a jelenség nem a védőoltás hibája. (Olyannyira, hogy a SIRV-modell példájában történetesen mind primer, mind szekunder értelemben tökéletes vakcina szerepelt!) Ez azon múlik, hogy az effektív reprodukciós szám nagyobb mint 1... de csak kicsivel. Hogy ez az átoltottság miatt van (mint a SIRV-modelles példánkban), a szekunder hatásosság miatt van (mint a komplexebb modelles példánkban), vagy valami más miatt van, az ilyen szempontból irreleváns. Ez nem a vakcina jóságával függ össze, hanem a fogékonyak összegyűlésének első ránézésre meglepő dinamikájával. Ettől még a védőoltási program lehet hatásos, ez abból is jól látszik, hogy a megbetegedettek száma – természetesen – a mézeshetes példákban kevesebb, mintha azért nincs mézeshét-effektus, mert rosszabb a védőoltási program (a példáinkban: kisebb az átoltottság, vagy gyengébb a szekunder hatásosság), a probléma tehát nem a megbetegedések száma, hanem azok váratlansága.
Térjünk most egy kicsit vissza a modelleink egyszerűsítő feltevéseire, a modellfeltevések valósághoz való közelítésére. Az egyik ilyen egyszerűsítő feltevés az volt, hogy a populáció struktúra nélküli, az alanyok tökéletesen keverednek. Mit jelent ez? A tökéletes keveredés következménye volt például, hogy azt mondhattuk: ha a lakosságnak összességében \(V\) hányada van beoltva, akkor egy adott fertőző beteg által a kórokozónak kitett emberek közül is épp \(V\) hányad lesz beoltva. Ez a valóságban nem így van, hiszen ha a megbetegedett fiatal, akkor nagyobb lesz az oltottak aránya (pláne egy nemrég bevezetett oltásból!) mintha idős lenne. Elképzelhető, hogy ha bizonyos iskolába jár, akkor kisebb lesz az oltottak aránya, mint máshol. Ha egy természetjáró klub tagja, akkor több lesz a kullancsterjesztette encephalitis ellen beoltottak aránya a környezetében mint egyébként. A tökéletes keveredés feltételezése ezeket zárja ki: azt mondja, hogy a populáció bármely tagja azonos valószínűséggel kerül kapcsolatba bármely másikkal – mintha mindenki egy teljesen szabadon mozgó golyó lenne egy nagy urnában, amit jól összerázunk. A valóságban ez persze nem így van; a feltételezés azért használatos mégis, mert lényegesen megkönnyíti a vizsgálódásainkat.
Nézzük most meg, hogy milyen következményei lehetnek annak, ha – persze az elemzés bonyolítása árán – figyelembe vesszük ezeket a finomabb tényezőket is.
Az egyik fontos ilyen, tökéletes keveredést sértő, struktúra az életkori struktúra: nem igaz, hogy teljesen véletlenszerű, hogy egy adott életkorú ember milyen életkorú emberekkel kerül kapcsolatba. Érezhető, hogy egy óvodáskorú sokkal gyakrabban kerül óvodáskorúakkal kapcsolatba, mint tizenévesekkel. Az érdekesség kedvéért megjegyzem, hogy erre vonatkozóan is végeztek tudományos alaposságú felméréseket, egy ilyennek mutatja az eredményeit a következő ábra. Gyönyörűen látszik, hogy a legkiemelkedőbb a bal alsó sarok-jobb felső sarok átló (minden életkorban a saját életkorbelieinkkel érintkezünk a legtöbbet, bölcsődétől iskolán és munkahelyen át az idősek otthonáig), de nagyon látványos, ahogy 30 év környékén megjelenik egy 0 évesekkel való kiemelkedés, akiknek az életkora aztán együtt nő...
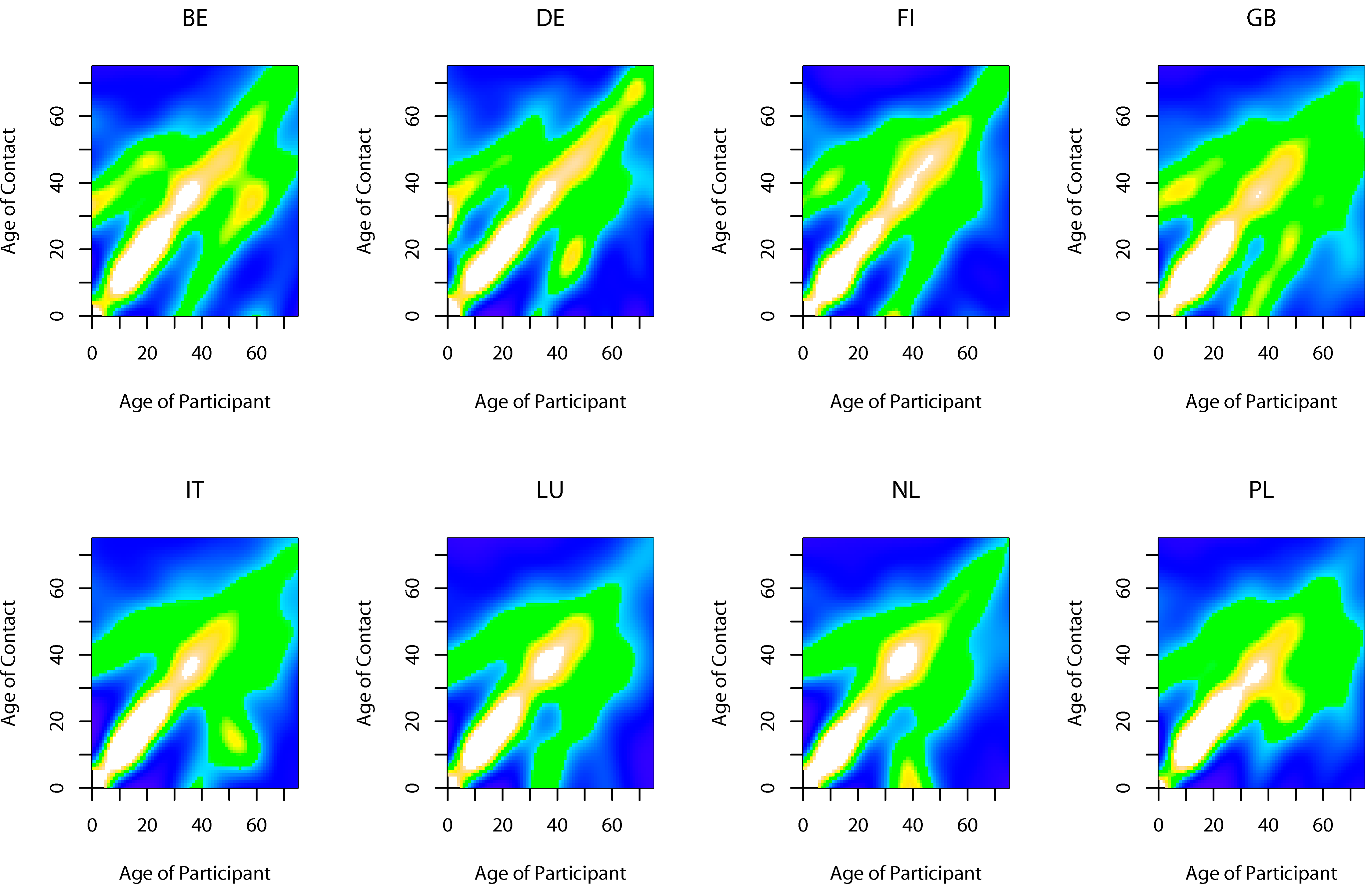Érintkezési mintázatok életkor szerint különböző európai országokban: minél világosabb egy pont, annál gyakoribb a kontaktus a pont koordinátái szerinti életkorú emberek között
Az ábra szerinti adatokat matematikailag egy ún. mátrixba szokták összefogni, melyet WAIFW-mátrixnak nevezünk (az angol 'ki kitől kapja meg a betegséget'-mátrix rövidítéséből). Hogy egész pontos legyek, a WAIFW-mátrixban az átvitelre jellemző ráták vannak – az egyes csoportok, például életkori kategóriák között időegység alatt mennyi betegség-átvitel történik –, amennyiben a megszokott értelmű reprodukciós számokat rakjuk egy mátrixba – egy adott csoportba eső alany hány másodlagos fertőzést generál egy másik csoportban, csupa fogékonyt feltételezve – akkor NGM-mátrixról beszélünk (az angol 'következő generáció mátrix' rövidítéséből). Az érdekes az, hogy az NGM-mátrixból kiszámolható egy mátrixalgebrai művelettel, hogy egy ilyen strukturált populációban összességében mi lesz a reprodukciós szám; egyfajta módon ki kell átlagolni a benne lévő, csoportok közötti reprodukciós számokat.
Az ilyen információk felhasználhatóak arra, hogy pontosítsuk a modelljeinket, például megbontva a halmazainkat ne egyszerűen fogékonyokról vagy épp fertőzöttekről beszéljük, hanem mondjuk 0-1 év közötti, 1-4 év közötti, 4-10 év közötti stb. fogékonyakról vagy fertőzöttekről. Ez értelemszerűen lényegesen megnöveli a modellezés bonyolultságát, de cserében a modell ilyen szempontból sokkal közelebb kerül a valósághoz – felhasználva az előbbi ábrához hasonló empirikus adatokat – javítva ezzel a leíró erejét; a gyakorlatban számos ilyen modellt használnak.
Ide kapcsolódik egy fontos megállapítás a szekunder hatásosság, azaz az oltások adta védelem gyengülése kapcsán. Bizonyos betegségeknél kiemelt érdek fűződik egy meghatározott életkorú csoport megvédéséhez, erre a szamárköhögés a tipikus példa, ahol a legkisebbek megvédése a legfontosabb, mert ők vannak különösen nagy, az idősebbeket sokszorosan meghaladó kockázatnak kitéve. Amennyiben az oltásunk nem ad rendkívül hosszú távú védelmet – sajnos a szamárköhögés elleni oltás, különösen a ma használatos, kevesebb mellékhatást okozó, de ezzel együtt kevésbé robusztus immunitást adó változata félő, hogy ilyen – akkor az eddigiekből úgy tűnhet, hogy nem tudunk nyájimmunitást kialakítani. Itt jön azonban a segítségünkre az életkori strukturálódás! Az egész populációban valóban elképzelhető, hogy nem tudunk nyájimmunitást kialakítani, de az előbbi ábrán látott jelenség lehetővé teszi, hogy "lokálisan", egy adott korcsoportban mégis csak létre tudjuk ezt hozni. Ha beoltjuk a kicsiket, de az oltás adta védelem gyorsan gyengül, akkor a tökéletesen keveredő modell szerint természetesen nem lesz nyájimmunitás, hiszen magasabb életkorra fogy a védelem, és a véletlenszerű keveredés miatt mindenki kapcsolatba fog kerülni magasabb életkorú – és így kevésbé vagy egyáltalán nem védett – emberekkel is. Csakhogy a valóságban nem ez történik! Nincs tökéletes keveredés, mint láttuk a kicsik elsősorban más kicsikkel fognak kapcsolatba kerülni – ám ők még gyengülő oltás adta védelem esetén is védettek lesznek, egyszerűen azért, mert ők sem rég kapták meg az oltást! Nagyon kicsiknél, újszülötteknél és csecsemőknél is hasonló a helyzet, annyi különbséggel, hogy ott nem az azonos életkorúak, hanem a szülők, testvérek, esetleg nagyszülők, nagynénik stb. jelentik a leggyakoribb kontaktust. És ez nem csak elméleti spekuláció: végeztek vizsgálatokat, melyek sziszifuszi munkával kinyomozták minden egyes csecsemőköri szamárköhögéses esethez, hogy a beteg pontosan kitől kapta meg a kórokozót, e vizsgálatok azt találták, hogy a forrás vagy a szülők valamelyike, vagy testvér, de mindenesetre közvetlen családtag az esetek legkevesebb kétharmad részében. Azért mondtam, hogy hasonló a helyzet, mert ez a kör nagyon szűk, így ez ismét csak lehetőséget ad egyfajta "lokális'" nyájimmunitás kialakítására, akár szekunder értelemben meglehetősen tökéletlen vakcinával is – ha az érintkező rokonokat a gyermek érkezése előtt be-(vagy újra-)oltjuk. Ez egyes országokban olyan népszerű stratégiává vált, hogy külön nevet is kapott: "cocooning" (magyarul fészekimmunizálásnak szokták fordítani). Ilyen módokon tehát még egy szekunder értelemben nem túl jó védőoltással is elérhető, hogy legalább a kimondottan veszélyeztetett csoportban fenn tudjuk tartani – kellő átoltottsággal, persze – a nyájimmunitást, még akkor is, ha az egész lakosságra vonatkozóan ez nem lehetséges.
Ez a gondolat más helyzetekben is megjelenik, egy tipikus példa az idős embereket gondozó egészségügyi dolgozók influenza elleni oltása. Az e mögötti logika az, hogy egyfelől ezek az idősek vannak – már pusztán életkorukból fakadóan, de gyakran az ilyen korban már nem ritka betegségeikből adódóan is – kitéve a legnagyobb influenza-kockázatnak, másfelől viszont épp náluk megyünk a legkevesebbre az oltással, hiszen – pont az előbbiek miatt – az ő immunrendszerük fog az oltásra is a legkevésbé reagálni. Mi a megoldás? Oltsuk be az őket gondozó egészségügyi dolgozókat! Náluk jobban fog hatni az oltás, hiszen fiatalabbak, egészségesebbek, és ha ezzel sikert érünk el, akkor indirekte megvédjük az időseket is, hiszen – megint csak "lokálisan", csak ezúttal nem életkor szerint, hanem egy adott intézményben – ki tudunk nyájimmunitást alakítani. Emlékezzünk vissza ugyanis a nyájimmunitás definíciójára: az a védettség, ami nem a szó szoros értelmében vett (immunológiai) védettségből fakad, hanem abból, hogy nincs kitől megkapni a betegséget – pont ezt érjük el, ha az idősekkel érintkező személyek mind védettek, márpedig közülük is a leggyakoribb kontaktust a gondozók jelentik. Sajnos az influenza elleni oltás még a szamárköhögés elleninél is sokkal megbízhatatlanabb, így e stratégia tényleges gyakorlati működőképességére vonatkozó eredmények vegyesek.
Van még egy, rendkívül érdekes (és népegészségügyileg is fontos) vetülete az oltási programoknak, ami a betegek életkor szerinti megoszlásával függ össze, ez pedig az oltási programok esetleges ún. paradox hatása. Ennek megértéséhez abból kell kiindulnunk, hogy egy oltási program elindítása megemeli a megbetegedéskori életkort. Ha azt az egyszerűsítést használjuk, hogy a lakosság korfája téglalap alakú – mindenki pontosan a születéskor várható élettartamig él, és akkor meghal – ami fejlett országokban nem nagyon rossz közelítés, akkor matematikailag levezethető, hogy a megbetegedéskori várható életkor \(\frac{L}{R_P}\), ahol \(L\) a születéskor várható élettartam. Ha tehát elkezdünk oltani, és ezzel lecsökkentjük \(R_P\)-t, akkor a megbetegedéskor várható életkort megnöveljük. De hát ez intuitíve is teljesen logikus: ha oltunk, és emiatt gyérül a kórokozó cirkulációja, akkor több idő fog várhatóan eltelni, amíg egy megszületett gyermek először találkozik a fertőzéssel. Ezen elmélet helyességét a gyakorlati adatok is alátámasztják:
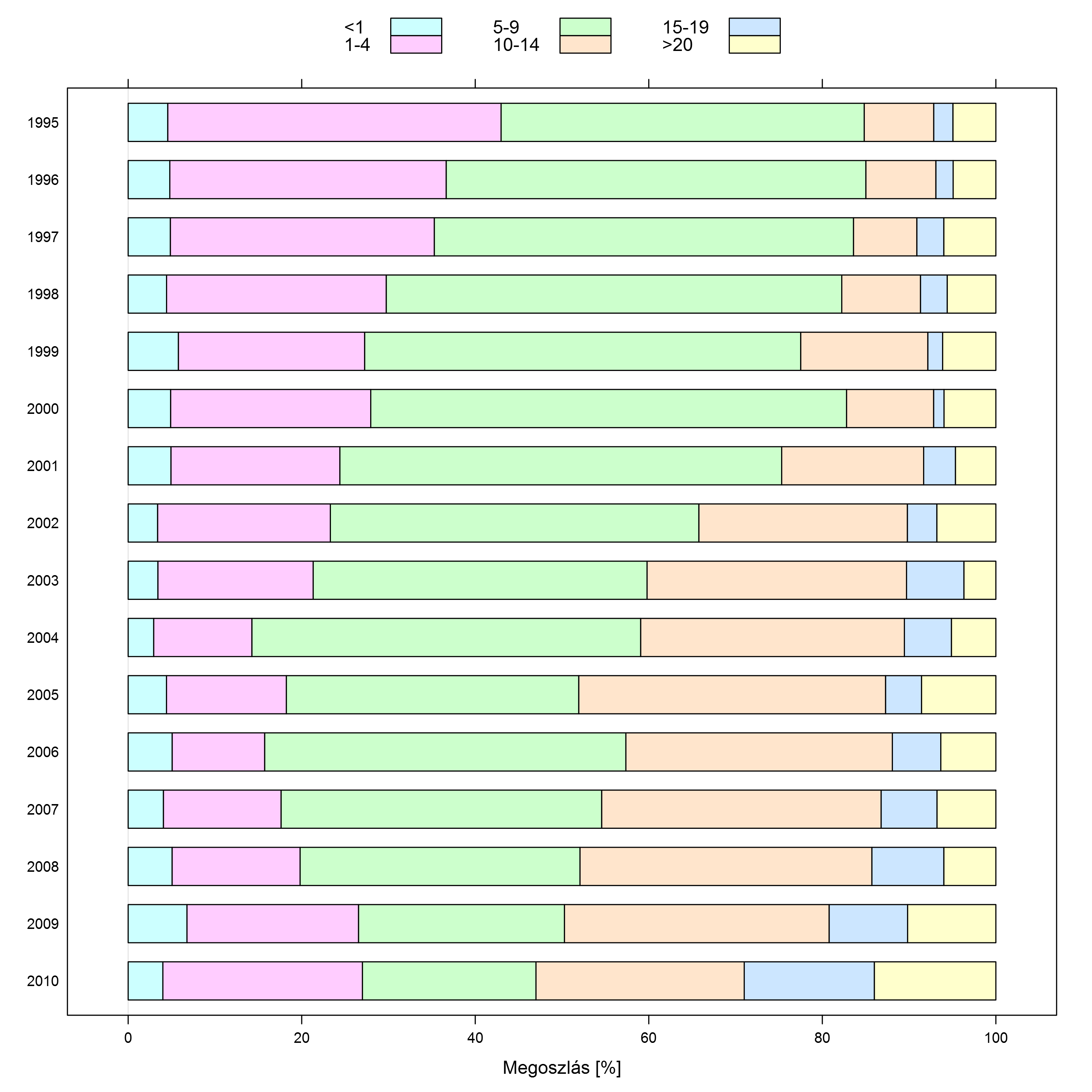Bárányhimlős esetek életkor szerinti megoszlása az Egyesült Államokban (Antelope Valley és West Philadelphia körzetek adatai)
Ez a jelenség semmilyen problémát nem okoz akkor, ha a betegség kockázata nem függ össze az életkorral, sőt, kimondottan jó is lehet abban az esetben, ha a kockázat életkorral csökken. Erre már szerepelt is nemrég egy példa, a szamárköhögés: ott nem csak, hogy nem baj, de kifejezetten jó hír a megbetegedések életkorának feltolódása, hiszen ez azt jelenti, hogy a legkockázatosabb életkorból kerülnek el a megbetegedések.
Baj lehet azonban akkor, ha a kockázat nő az életkor emelkedésével! Erre két klasszikus példa van: a bárányhimlő (melynek minden komplikációja sokkal-sokkal gyakoribb felnőttkorban) és a rubeola (mely a várandós nők magzataira nézve jelent kockázatot, ugyanis a magzat veleszületett rubeola szindrómáját okozhatja). Nézzük meg a helyzetet a rubeola példáján! Ha beindítjuk az oltási programot, az csökkenti a megbetegedések várható számát, ám azok kockázatosabb életkorba, a gyermekvállalás felé tolódnak. Mi lesz az összesített hatás, azaz hogyan változik a veleszületett rubeola szindrómák száma? Bármilyen furcsa is lehet elsőre, de ezt nem lehet ránézésre megmondani! A dolog azon múlik, hogy melyik faktor az erősebb: a veleszületett rubeola szindrómák száma az össz-esetszám és a kockázatos életkorba esés arányának a szorzata, az oltás az előbbit csökkenti, az utóbbit növeli, így a dolog azon múlik, hogy melyik hatás lesz erősebb. Ezt nem lehet ránézésre megmondani, adott esetben az is elképzelhető, hogy bizonyos szerencsétlen paraméter-kombinációk mellett az utóbbi a nagyobb hatású, és így az oltási programmal végeredményben megnöveljük a megelőzni kívánt megbetegedések számát! Ezt hívjuk a vakcináció paradox hatásának.
A már látott epidemiológiai modellekkel ez a kérdés számszerűen is megvizsgálható. A következő ábra mutatja, hogy hogyan alakul a veleszületett rubeola szindrómás esetek száma az átoltottság függvényében (minden értelemben tökéletes vakcina mellett is!). Figyelem: az ábrán nem a rubeolás esetek várható száma van (az mindenképp csökken!), hanem a veleszületett rubeola szindrómás esetek száma!
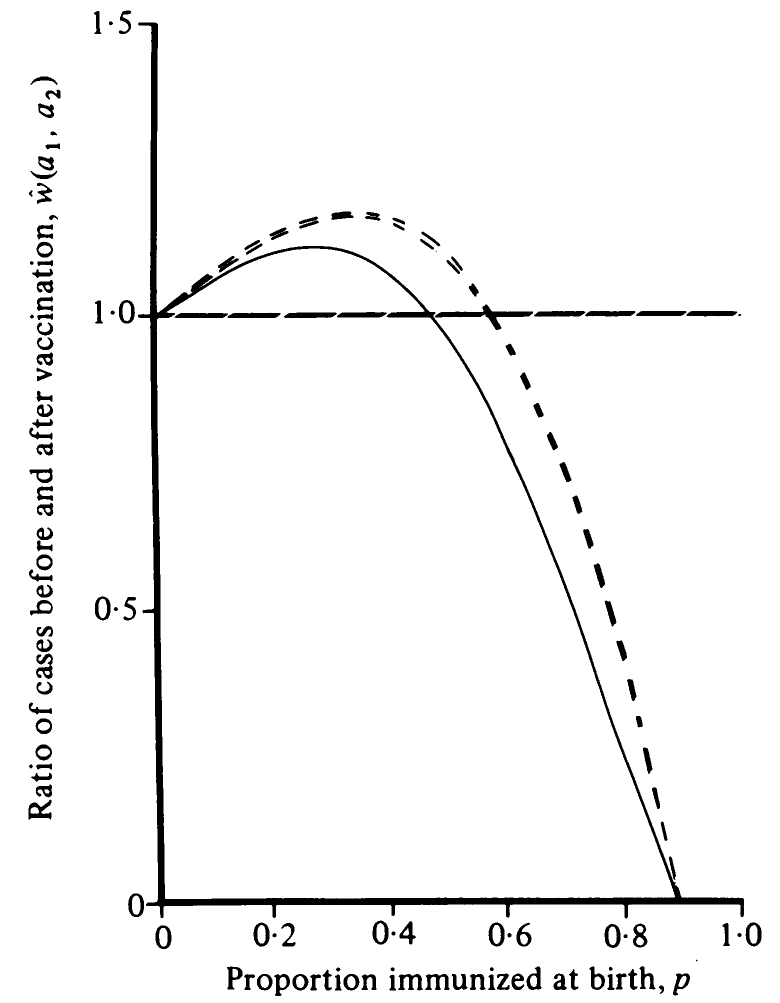Veleszületett rubeola szindrómás esetek száma (pontosabban szólva a 16 és 40 év közötti rubeolás esetek száma, de a veleszületett rubeola szindrómák száma ezzel jól korrelál) az oltás bevezetése előtti állapothoz viszonyítva a rubeola elleni átoltottság függvényében, tökéletes vakcinát tételezve fel (a különböző görbék ahhoz tartoznak, hogy mit feltételezünk a lakosság korfájának alakjáról), egy epidemiológiai modell alapján
Látható, hogy ha elég nagy arányban oltunk, akkor az össz-esetszám csökkenése nagyobb hatású, mint az esetek életkorának feltolódása, és így a veleszületett rubeolás esetek száma is csökken (a rubeolás eseteké ugye mindenképp). Külön felhívom a figyelmet arra, ami 85% környékén történik: ez a nyájimmunitás, amit korábban már alaposan kiveséztünk – ezt a szintet elérve nem egyszerűen tovább csökken az esetszám, hanem egzaktan nullába áll, mivel ekkor már nem tud önfenntartó járvány kitörni.
Ami igazán érdekes, az a grafikon bal oldala: ha oltunk ugyan, de csak kicsit, akkor az életkor-eltolódás nagyobb hatású mint az esetszám csökkenése – azaz többet ártottunk, mint használtunk! Ez a vakcináció paradox hatása.
Az ábrán látottak bizonyos szempontból meglepőek, de bizonyos szempontból azért megnyugtatóak. Meglepő eleve, hogy egyáltalán létezik ez az effektus, sokan nem gondolnának erre. Nem véletlenül tárgyaltam ezt ebben a fejezetben: ez is egy olyan jelenség, ami csak akkor érthető meg, ha nem csak az oltás direkt (adott alanyra gyakorolt) hatását nézzük, hanem az indirekt hatását is – ez is azon múlik, csakúgy mint a nyájimmunitás, hogy az oltás nem csak az egyént, hanem az egész közösséget is befolyásolja. Meglepő az is, hogy ez nem valamiféle elhanyagolható apróság: a paradox hatás, tehát a magzati rubeolakárosodás szaporodása akár egészen 40-50%-os átoltottságig is jelentkezik! Ott kezd el az össz-esetszám csökkenése felülkerekedni, és kompenzálni az életkori eltolódás hatását. Másrészt viszont megnyugtató is ez az eredmény: ahhoz képest ugyanis nem sok a 40-50%, amennyit el lehet érni a fejlett országok körülményei között az oltási programmal.
Itt érdemes egy fogalmat bevezetni: a szelektív és univerzális oltási stratégia fogalmát. A rubeola példáján szemléltetve: a fenti eredmények miatt a '70-es, '80-as években néhány ország csak a rubeolán természetes fertőzéstől át nem esett, serdülőkorú lányokat oltotta (szelektív oltási stratégia). Ez ugyanis elkerüli a fenti problémát: mivel fenntartja a rubeola természetes cirkulációját – a kisebb lányok és az összes férfi révén – így a megbetegedéskori életkor nem fog lényegesen feltolódni. Hátránya, hogy soha nem lehet vele elérni a veleszületett rubeola szindróma teljes felszámolását (hiszen mindig lesz lány, aki az oltás előtt esik, nem tervezetten, teherbe, az oltás nem tökéletesen hatásos, így lesz aki oltás ellenére is védelem nélkül marad stb.). Ezt a teljeskörű védelmet csak úgy lehet elérni, ha a nyájimmunitást próbáljuk kialakítani – ahhoz viszont nagy átoltottságra kell törekedni, mindenki oltását megcélozva (univerzális oltási stratégia). (Tehát fiúkat is oltva – igaz, hogy a betegségtől csak lánynak lehet baja, de elkapni fiútól is lehet!) Így – és csak így –, tehát a cirkuláció felszámolásával érhető el a valós nulla szövődmény-előfordulás; pontosan ezért, mivel a fenti 40-50%-os átoltottság elérhető, szinte minden ország áttért évtizedekkel ezelőtt az univerzális stratégiára. Mivel rubeola ellen szerencsére – primer és szekunder értelemben egyaránt – igen hatásos vakcinával rendelkezünk, így a fejlett világon elsöprő sikert hoztak az univerzális stratégián alapuló oltási programok. (Magyarországon 1990 óta összesen nem fordult elő 10 veleszületett rubeola szindrómás eset.)
Ellentmondásosabb a helyzet a bárányhimlő esetében. Nem kis részt amiatt, mert jelenleg még nem ismert biztosan a védőoltás szekunder hatásossága, ebben a kérdésben nincs konszenzus. (Az, hogy a nagy átoltottságú helyeken hosszú évek óta szinte eltűnt a betegség, a mézeshetek-effektus miatt nem perdöntő, ráadásul még ezeken a helyeken is exponálódtak az oltottak természetes bárányhimlőnek is, frissítve az immunitásukat.) Az eldöntendő kérdés persze itt is ugyanaz: az univerzális stratégiával (és csak azzal) lehet elérni a valós nulla szövődményszámot, de kockázatot vállalunk, ha kiderül, hogy az oltás mégsem olyan jó szekunder értelemben, és visszatér a betegség – csak immár a sokkal kockázatosabb életkorúak körében. A szelektív stratégia csak a szövődmény-kockázatnak kitett csoportokat oltja (hogy ezzel levágja a szövődmények számának oroszlánrészét), a többiek körében meghagyja a cirkulációt. Sajnos mivel nem tudjuk teljesen biztosan megmondani előre, hogy ki van kitéve a szövődmények kockázatának, így ezzel a stratégiával soha nem fogunk tudni elérni nulla szövődmény-előfordulást, de cserében részesülünk a fenntartott cirkuláció előnyeiből (ideértve azt is, hogy az oltottak – tehát épp a legveszélyeztetettebbek – védelme is jobb lesz a természetes "frissítés" miatt). Ami viszont biztos, hogy a kettő között kell választani: vagy csak célirányosan a kockázati csoportokat oltjuk (azaz összességében keveseket), vagy lehetőleg mindenkit – de a kettő közötti megoldásokból baj lehet (mivel többet vesztünk az életkori eloszlás eltolódásával, mint amennyit nyerünk az esetszám csökkenésével). Pontosan ezért van az, hogy a vonatkozó WHO-ajánlás is azt mondja, hogy fejlett országokban a bárányhimlő elleni oltási kampányoknak vagy legfeljebb 30%-os vagy legalább 80%-os átoltottságra kell törekedniük. De hogy a kettő közül melyik a jobb, abban még az elméleti és gyakorlati szempontból legfelkészültebb népegészségügyi rendszereket működtető országokban sincs egyetértés: az Egyesült Államok univerzálisan olt, Anglia szelektíven.
Végezetül érdemes megjegyezni, hogy természetesen az életkori – és egyéb – egyszerű struktúrák figyelembevétele sem jelenti az emberek közti kapcsolatok tökéletes leírását. Az, hogy ki kivel kerül kontaktusba, igen bonyolult a valóságban, van, aki sokakkal, van aki kevéssel, ennek szabályszerűségeire meglehetősen komplex vizsgálatokat folytattak. Ezt igyekszik megragadni az epidemiológia egy új, izgalmas ága, az ún. gráf-modellek, a hálózatelemzés eszköztárának az alkalmazása. Ezeket a modelleket úgy kell elképzelnünk, mintha minden embernek megfeleltetnénk egy pontot egy lapon, és két pontot (embert) akkor kötünk össze, ha köztük – az adott fertőzés átadására alkalmas – kontaktus van. Az ilyen, pontokból és a köztük húzódó élekből álló hálózatokat hívják a matematikában gráfnak.
Ez elvi szinten elég kézenfekvő, ám egy ilyen gráf gyakorlati megkonstruálása, tehát az emberek közti tényleges kapcsolatok feltárása igen nehézkes. Hogyan gyűjtsük be ezeket az adatokat? Fel tudják egyáltalán idézni az emberek, hogy kivel kerültek kapcsolatba? El is akarják ezt nekünk mondani (gondoljunk a szexuális úton terjedő betegségekre is!) egy ilyen vizsgálatban? De még ha ezektől el is tekintünk a hálózat definíciója sem olyan egyszerű, mint gondolnánk. A problémák ott kezdődnek, hogy a valóságban nem beszélhetünk "a" hálózatról, ami alanyaink között van, hiszen – ahogy arról már korábban is volt szó – eltérő kontaktusok kellenek az eltérő betegségek átadásához – tehát adott, rögzített csoport tagjai között is annyi hálózatot rajzolhatunk, ahány betegséget vizsgálunk! Nyilván más hálózat fog tartozni egy szexuális úton terjedő és egy cseppfertőzéssel terjedő betegséghez (azzal, hogy az előbbi részhalmaza lesz az utóbbinak), de még a cseppfertőzéssel terjedő betegségeknél sem mindegy, hogy kanyaróról vagy mumpszról van szó – a problémát természetesen az jelenti, hogy milyen szorosságú kapcsolat kell egy fertőzés átadásához. Mivel ez jellemzően még így is csak valószínűségi alapon mondható meg (sokszor nem fogjuk tudni megmondani biztosan, hogy egy kapcsolat alkalmas volt-e a betegség átadására), egy lehetséges megoldás a hálózat súlyozása. Ez azt jelenti, hogy minden élre felírjuk, hogy az adott kapcsolat mekkora valószínűséggel volt alkalmas a betegség átadására – minél szorosabb volt a kapcsolat, annál nagyobb lesz ez a súly. Ez ugyan az előbbi problémát megoldja, azonban rögtön generál egy másikat: így már ezeket a valószínűségeket is meg kell határozni. Ha már az is bizonytalan, hogy mennyire emlékszünk arra, hogy kivel kerültünk egyáltalán kapcsolatba, akkor az mennyire lesz biztos információ, hogy milyen szoros kapcsolatban voltunk? És egyáltalán, hogyan tudjuk ezt pontosan definiálni, hogyan tudhatnánk valaha is olyat mondani, hogy mondjuk egymástól 23,5 centiméterre volt a fejünk 2 perc 13 másodpercen keresztül, ami alatt az egyik fél köhögött, akkor 73,8% valószínűséggel jutott át ez a cseppfertőzéssel terjedő betegség...?
Egy szó mint száz, az ilyen hálózatok tényleges megkonstruálásának rengeteg problémája van, és az eredmény nagyon erősen fog múlni azon, hogy pontosan milyen definíciókat alkalmazunk az adatgyűjtés során. Mindazonáltal a gyakorlatban – épp az ilyen információ értékessége miatt – a nehézségek ellenére is számos vizsgálatot folytattak, mely a betegségek terjedését lehetővé tevő hálózatok feltárását irányozta. Alapvetően három módszer alkalmazása jöhet szóba: a megbetegedettek esetén a fertőzés forrásának és az adott beteg által megbetegített további személyeknek a felkutatása (ez a legegyszerűbben kivitelezhető, hiszen közel áll ahhoz, amit a népegészségügyi szervek amúgy is tesznek egy járvány kitörésekor, cserében nem tudja az egész hálózatot feltárni, hiszen abban az összes átadásra alkalmas kapcsolat kellene, hogy szerepeljenek, itt pedig csak a ténylegesekről lesz információ); a megbetegedett személy – lehetőleg a járvány kiindulópontja – összes kapcsolatának felkutatása, a közülük fertőzöttnek bizonyulók összes kapcsolatának felkutatása és így tovább (ez még mindig nem ad képet a teljes hálózatról, hiszen a nem fertőzöttek kapcsolati rendszeréről nem lesz információnk, de azért a legfontosabb részekről jó képünk lesz, cserében jóval munkaigényesebb is, mint az előző megoldás); és végül a harmadik lehetőség, hogy az alanyainkat megkérjük, hogy vezessenek naplót a kontaktusaikról (ez már teljes képet ad a hálózatról, eltekintve attól a nehézségtől, hogy a különböző alanyok naplóit hogyan tudjuk összekapcsolni, cserében bejön az összes korábban felsorolt probléma).
Egy gyakorlati példát mutat egy ilyen módszerekkel feltárt hálózatra a következő ábra.
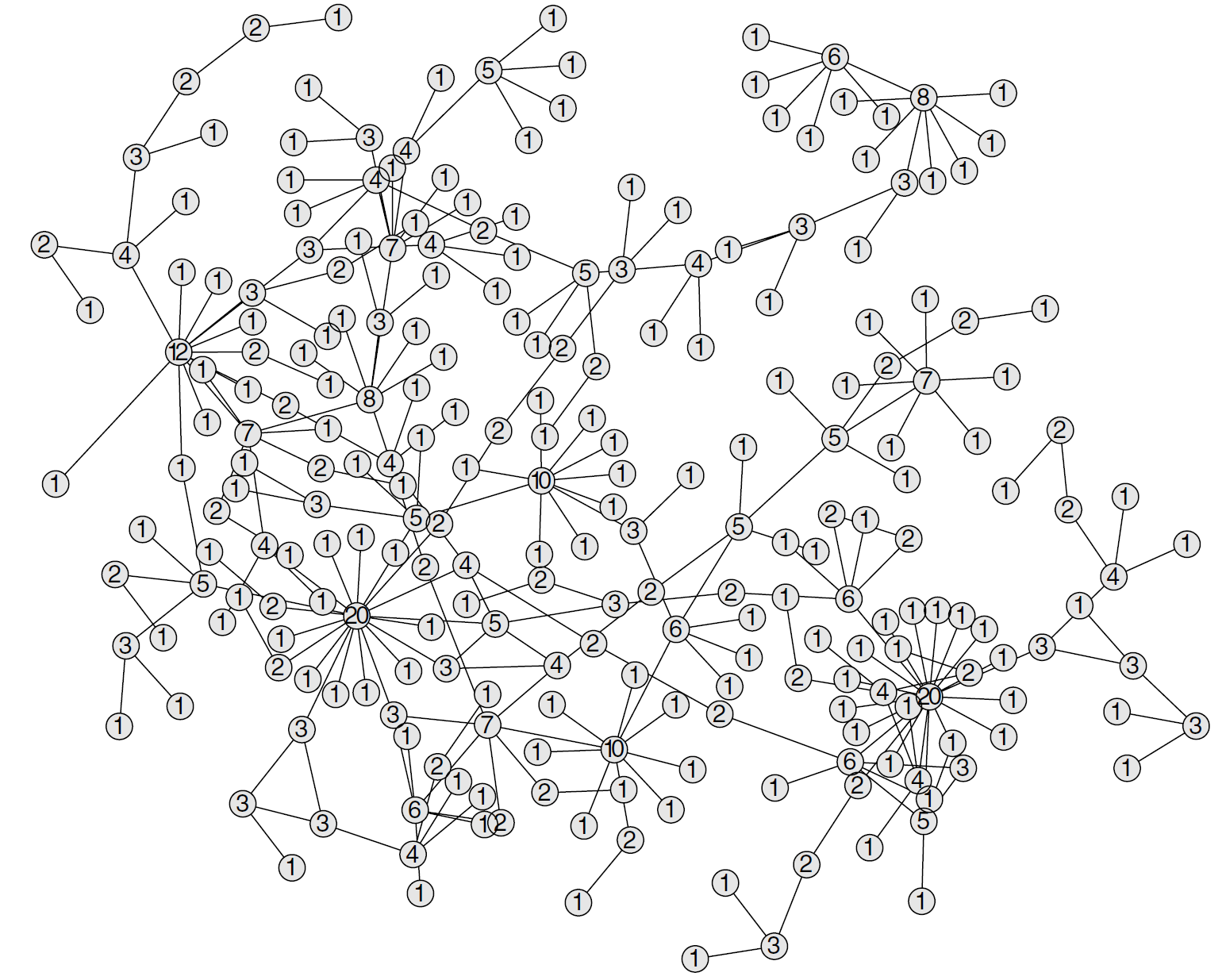
Az amerikai Colorado Springs városában kitört HIV/AIDS-járvány kapcsolati hálója (1980-as évek). Minden pont egy személy, két személy össze van kötve, ha köztük fertőzés átadására alkalmas kapcsolat valósult meg (a pontokra írt számok a kontaktusok számát jelzik). A hálózat összeállítása a 'fertőzöttek kontaktusainak felkutatása, és a köztük fertőzöttnek bizonyulók kontaktusainak felkutatása és így tovább' metodikával történt, azaz a nem fertőzöttek kapcsolatairól nincs információnk.
Nagyon érdekes kérdés, hogy ezek a hálózatok milyen tulajdonságokkal rendelkeznek – ha már egyszer megvan a hálózatunk, akkor ennek elemzésére jól ismert eszközkészlet áll rendelkezésre, hiszen a hálózatelemzés tudománya sokkal korábban kifejlesztett egy komplett apparátust erre, "mindössze" át kell ezt emelni az epidemiológia területére. Az előbbi ábrán például jól látszik, hogy van pár központi, sok kapcsolattal rendelkező ember és kisebb számú "távoli" kapcsolat. E jelenség lemérésére rendelkezésre állnak mutatók, melyeknek csak meg kell adnunk – alkalmas számszerű leírással – a hálózatot, és azonnal jellemzik, hogy mennyire áll fenn ez a tendencia. Hasonlóan elérhetőek mutatók arra, hogy milyen útvonalak vannak az egyes emberek között, esetleg elkülöníthetőek-e komponensek a gráfban, mennyire központi az egyes emberek szerepe és így tovább.
A gráf-modelleken alapuló epidemiológia másik fő csapásiránya a hálózatok idealizálása. Ha megnézünk számos valós hálózatot, akkor azt látjuk, hogy azok mind-mind különböznek egy sor partikuláris részletben, de egy idő után az is fel fog tűnni, hogy alapstruktúrájukban viszont vannak azonosak. Adódik tehát a gondolat, hogy próbáljunk absztrahálni, azaz megtisztítani a hálózatokat a konkrét részletektől, és kikristályosítani bizonyos – ideális – alaptípusokat. Ilyenekre mutat példákat a következő ábra.
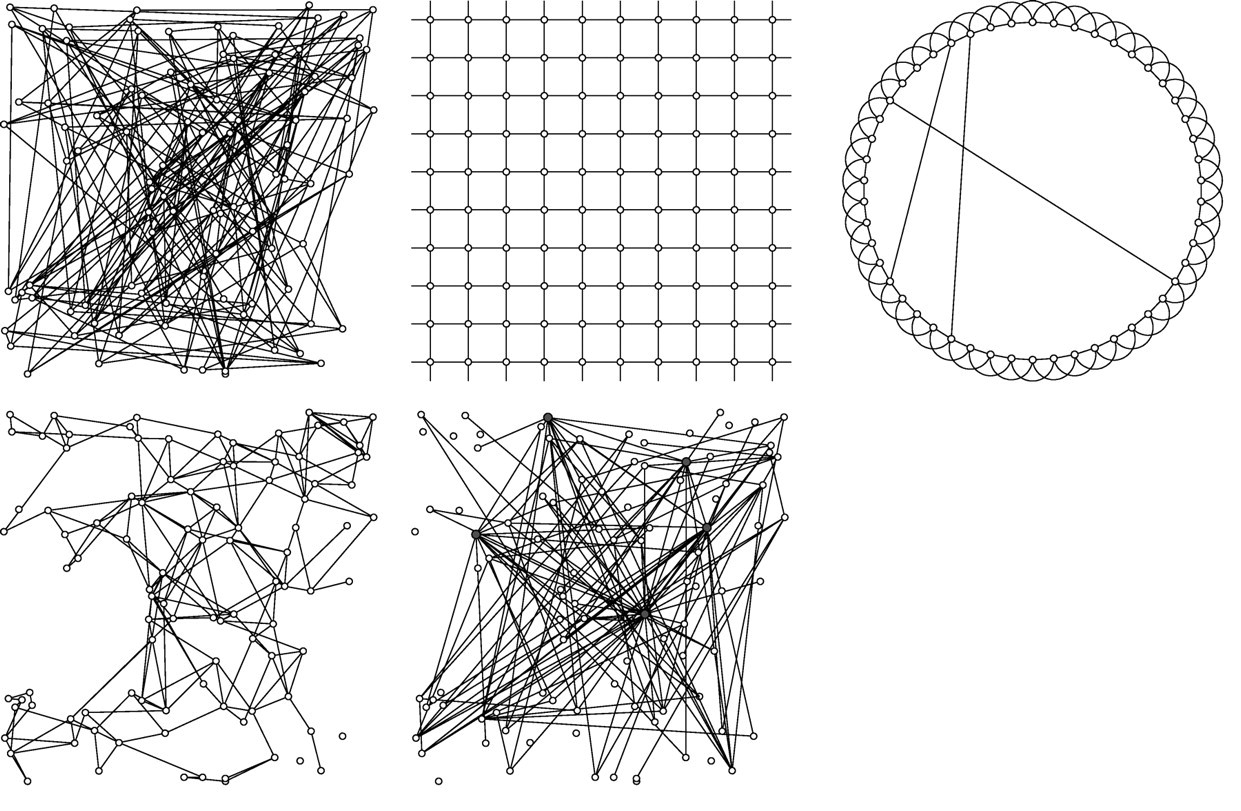Néhány példa az emberek közti kapcsolatokat leíró gráf-modellekre, balról jobbra haladva és a felső sorból indulva: teljesen véletlen gráf, szabályos rács, "kis világ" hatású gráf (szabályos rács, kiegészítve kis számú, de nagy távolságot átugró véletlen kapcsolattal, melyeknek köszönhetően kevés lépéssel elérhető bármelyik pontból indulva bármelyik másik pont), térbeli strukturálódású gráf (a fizikailag közel lévő pontok között nagyobb valószínűséggel húzódik kapcsolat), skálafüggetlen gráf (a pontok kis részének sok kapcsolata van, nagy részének pedig kevés).
Ez azért nagyon hasznos, mert lehetővé teszi a kérdés matematikai tisztaságú kezelését, hiszen ezek az alaptípusok már pontosan ismertek, matematikai úton leírhatóak. Megtehetjük, hogy paramétereiket úgy állítjuk be, hogy a kiadódó hálózatok a valóságban látottakhoz hasonlítsanak, csak míg azok mögött nem tudjuk milyen modell van, ezeknél igen, hiszen mi hoztuk őket létre, és így tulajdonságaik – elméleti levezetéssel vagy szimulációval – jól vizsgálhatóak.
Az előbb úgy fogalmaztam, hogy "nagyon érdekes kérdés, hogy ezek a hálózatok milyen tulajdonságokkal rendelkeznek" – a másik, nem kevésbé érdekes kérdés, hogy ezek a tulajdonságok milyen kapcsolatban vannak a kitörő járvány jellemzőivel! Az epidemiológia hálózatelemzésen alapuló ága arra is kísérletet tesz, hogy az emberek közötti kapcsolatokat leíró gráfok tulajdonságaival összefüggésbe hozzák az ilyeneken terjedő járványok jellemzőit. Ha ezt megválaszoljuk, akkor sokkal valósághűbb ismereteket tudunk nyerni a járványokról, előrejelezni oltási programok hatását stb., azáltal, hogy az emberek közti kapcsolatokat realisztikusabban rakjuk bele a modellbe.
Visszatérve a tökéletes keveredésre, egy másik tipikus sérülése ennek, hogy azt feltételezi, hogy a nem védettek egyenletesen oszlanak meg a védettek tengerében. Ha nem ez a helyzet, hanem térben koncentrálódnak, akkor a fenti okfejtés felborul. Erre jó példa, hogy egyes nyugat-európai országokban annak ellenére ki tudnak törni kanyarójárványok, hogy az egész ország szintjén számolva egyáltalán nem rossz, 90% körüli vagy akár fölötti az MMR-átoltottság. Ha azonban jobban megnézzük – erre a kérdésre később még részletesen is kitérek –, akkor láthatjuk, hogy ezek a járványok tipikusan olyan helyeken törnek ki, például bizonyos iskolában, ahol helyileg (az adott iskola tanulói körében) jóval kisebb az átoltottság, azaz térben csoportosulnak a nem védett gyermekek.
Az eddigieket összefoglalva: a legtöbb védőoltással megelőzhető fertőző betegség, illetve védőoltás esetén van egy – a pontos körülményektől függő értékű – minimális átoltottság, amit el kell érni ahhoz, hogy fennálljon a nyájimmunitás. Ha ez kialakul, akkor azok sem tudják a betegséget megkapni, akik nem védettek, mert nem lesz kitől.
Ez ma Magyarországon a helyzet a kanyaró, a rubeola stb. esetén – szemben például Németországgal, Franciaországgal vagy Svájccal. Ezért van az, hogy ma Magyarországon gyakorlatilag nincs kanyaró, rózsahimlő stb., noha természetesen nem védett mindenki ezekkel a betegségekkel szemben. Vannak és mindig lesznek olyan emberek, akiket a legnagyobb jóindulattal is lehetetlen megvédeni az oltással, vagy azért, mert nem vált ki kellő választ náluk az oltás (hiszen semelyik oltás nem 100%-os hatásosságú), vagy azért, mert nem adható nekik oltás. Ez utóbbi oka, hogy minden oltásnak léteznek kontraindikációi, melyek közül a legfontosabbak:
- Várandós nő élő ágenst tartalmazó oltást tervezetten nem kaphat; élő ágenssel végzett immunizáció után lehetőség szerint 3 hónapig kerülni kell a teherbeesést. Bármilyen oltást is csak akkor kaphat várandós nő, ha a fertőzés kockázata kifejezetten és lényegesen magasabb, mint az oltás általában vett mellékhatás-kockázata (pl. veszettségre gyanús állat harapása esetén veszettség elleni oltás).
- Hasonlóképp átmenetileg nem olthatók a lázas betegek.
- Sok oltás beadása minimális életkorhoz kötött, az ennél fiatalabbak nem védhetők meg vakcinával.
- Olyan személy, aki valamely oltásra súlyos nemkívánatos eseménnyel (pl. anafilaxiás reakció, encephalitis) reagált, később ugyanolyan oltóanyaggal nem oltható.
- Olyan személy, aki az oltás bármely összetevőjével való korábbi érintkezésre súlyos túlérzékenységi (anafilaxiás) eseménnyel reagált, az adott oltóanyaggal nem oltható.
- Immunhiányos betegek élő vakcinával általánosságban véve nem olthatóak, ugyanis a vakcinában lévő élő kórokozó elszaporodhatna a szervezetükben, és betegséget okozhatna. Ide tartoznak egyes immundeficiens betegek, illetve azok, akik valamely okból (pl. szervátültetés) terápiásan immunszupprimáltak. Nem élő kórokozót tartalmazó oltást általánosságban kaphatnak, mert ott ez a biztonságossági probléma nem áll fenn, viszont ott meg sajnos a hatásossággal van baj: tipikus, hogy az immunrendszerük kevésbé tud reagálni az oltásra, így bár bajuk nem lesz tőle, de hatni sem hat megfelelően. Gyakori, hogy ilyen oltásokból még többet is adnak nekik, mint az egészségeseknek, de a kiváltott védelem sajnos így sem éri el azt, amire egészséges immunitású embernél képes az oltás.
Ők saját immunrendszerükön túlmenően csak a társadalom többi tagjára, a nyájimmunitásra számíthatnak! A felelősségünk az ő irányukban is fennáll.
Hadd hozzak egy – talán kevésbé közismert, de mellbevágó – példát a nyájimmunitásra. Ennek alanya a Streptococcus pneumoniae nevű baktérium, amelyik több csúnya betegséget is tud okozni (nevével ellentétben nem csak tüdőgyulladást, hanem agyhártyagyulladást, középfülgyulladást és sok egyebet); 2000 óta elérhető ellene védőoltás. Nézzük meg most}, hogy hogyan alakult az S. pneumoniae okozta agyhártyagyulladásos megbetegedések száma az Egyesült Államokban! A két évnél fiatalabbak körében az incidencia az oltás bevezetése előtti év 10 per 100 ezerjéről leesett 3,7 per 100 ezer körülire (mindössze 5 év alatt!), azaz 64%-kal csökkent. Eddig még nincs semmi érdekes, ez az oltás közvetlen hatása. Az igazán meglepő most jön: az oltás bevezetését követően a 65 év feletti korosztályban – akik tehát nem is részesülhettek oltásban – is hirtelen zuhanni kezdett az S. pneumoniae okozta meningitis incidenciája: ugyanez alatt az ötéves időszak alatt hirtelen 54%-kal csökkent! Hangsúlyozom: ők az oltás közelében nem jártak! Akkor vajon ez mitől van...? A válasz nagyon egyszerű: a védőoltás igen erősen lecsökkentette a S. pneumoniae baktérium hordozását a gyermekek körében, így bár az idősek magától a vakcinától természetesen semmilyen védelmet nem kaptak, de a védőoltásnak köszönhetően kevésbé volt kitől elkapniuk a betegséget! Végeredményben tehát a védőoltás nem csak azokat védte, akik megkapták, hanem az egész lakosságot. (Ebben az is szerepet játszik, hogy ennél a baktériumnál elég gyakori a tünetmentes hordozó állapot, azaz az emberek egy részéből kitenyészthető a S. pneumoniae anélkül, hogy bármi bajuk lenne. Aztán egyszer csak invazívvá válik, és megöli a gazdáját. Vagy átugrik másra, és megöli azt. Ez teljesen kiszámíthatatlan; viszont a védőoltás kiürítette a betegségnek ezeket a rezervoárjait, így védte meg a nem is oltott időseket is.)
És ez a tömeges vakcináció igazi értelme: bár nem olthatunk be mindenkit, és a kialakított védelem még a beoltottakban sem tökéletes, de szerencsére nem is kell annak lennie: ha elég sok embert be tudunk oltani ahhoz, hogy még ezzel a bizonytalansággal együtt is meghaladjuk a kritikus átoltottságot, akkor az össztársadalmi védelem ugyanúgy szinte tökéletes lesz, mintha mindenkit beoltanánk, és az egyéni védelmek tökéletesek volnának.
És ez az, amit a védőoltás-ellenesek veszélyeztetnek. Itt tehát nem arról van szó, hogy "miért ne dönthetnék úgy, hogy nem oltatom be a gyermekemet, mást úgysem veszélyeztetek ezzel, legyen ez az én dolgom", ugyanis egy ilyen döntés igenis veszélyeztethet másokat. Ez az okfejtés legfeljebb addig lehet igaz, bár ott sem tökéletesen, amíg az ilyen nem-oltásokkal együtt is felette vagyunk az össznépességi védelemhez szükséges szintnek. Viszont, ha valamiért – például a védőoltás-ellenesek terjesztette tévhitek és félrevezető közlések miatt... – az átoltottság e szint alá esik, akkor kitörnek a járványok (ahogy az Németországban, Svájcban, Franciaországban stb. ténylegesen meg is történt és történik). Ezek ugyan többségében oltatlanokat érintenének, de egyrészt, mivel egyetlen oltás sem 100%-os hatásosságú, oltottakat is, másrészt az oltatlanok egy része sem saját döntése miatt oltatlan, hanem "önhibáján kívül" nem oltható, mert beteg, fiatal stb. Az ő megbetegedéseikért a védőoltás-ellenesek lennének a felelősek, ezért nem hivatkozhatnak egyszerűen arra, hogy "ők nem befolyásolnak másokat, csak azt szeretnék, ha békén hagynák őket". E kérdésekkel a kötelezőség kapcsán fogok még hosszabban foglalkozni.
