Jelen fejezetben egy olyan kérdésről lesz szó, mely tulajdonképpen sokkal általánosabb, akármilyen gyógyszer (vagy egészségügyi eljárás) kapcsán elmondható lenne, de a védőoltásoknál különösen fontos a szem előtt tartása: a kockázat-haszon mérlegelés. Elsőként bevezetem az alapgondolatot, majd utána két speciálisabb részkérdést tárgyalok meg.
A kockázat-haszon mérlegelés alapgondolata
Ritka kivételektől eltekintve egy gyógyszer, vagy egyáltalán, bármilyen egészségügyi célú eljárás (gyógytea megivásától a szívátültetésig) alkalmazásáról szóló döntés mérlegelésen alapszik. Ez azt jelenti, hogy szembesíteni kell egymással a várható előnyöket és a várható hátrányokat, majd ezek egybevetésével dönteni. A hatásosság és a biztonság fogalmak nem értelmezhetőek önmagukban: bár szoktunk olyat mondani, hogy "ez a gyógyszer biztonságos", valójában ez legjobb esetben is egy pongyola kifejezés, hiszen ez egy relatív fogalom – a mellékhatások csak akkor értékelhetőek, ha viszonyítjuk őket ahhoz, hogy mit érünk el cserében. Akár ugyanaz a gyógyszer is lehet nagyon biztonságos (ha egy nagyon súlyos állapotú beteget megmentünk vele) és egyáltalán nem biztonságos (ha egy banális betegséget csak félig-meddig gyógyítunk vele)! Ezek a fogalmak csak relatíve, összehasonlításban értelmezhetőek.
Amiből tehát ki kell indulni: hogy milyen hatásai és milyen mellékhatásai lehetnek a gyógyszernek. Nagyon sokan azt gondolják, hogy az alkalmazásról szóló döntésben ezeket kell összevetni. Ez nem igaz! Van ugyanis egy harmadik szempont, amit szintén nem hagyhatunk figyelmen kívül: a gyógyszer be nem adásának hatásai és mellékhatásai. Csak így teljes a kép. Valójában tehát a gyógyszer hatásain és mellékhatásain kívül egy harmadik információra is szükségünk van: a kezelés elmaradásakor várható történésekre. Ezek már lehetővé teszik a megalapozott döntést. A legegyszerűbb, ha azt tartjuk mindig szem előtt, hogy két dolgot kell összevetnünk: a várható történéseket a gyógyszer beadásakor és a várható történéseket a gyógyszer be nem adásakor (vagy az eljárás alkalmazásakor). Dönteni az alapján kell, hogy e kettő közül mi az előnyösebb. Ez a kockázat-haszon mérlegelés.
E probléma egyik jellemző nehézsége a sztochasztikus jellege: a legtöbb esetben nem bizonyosak a történések, csak lehetséges kimeneteink vannak, amelyek valamilyen valószínűséggel következnek be. A kimeneteket magukat összegyűjteni, és a valószínűségeiket megbecsülni szisztematikus adatgyűjtésekkel lehet (noha bizonyos esetekben, például a gyógyszer ritka mellékhatásainál, a pontos számszerűsítés igen nehéz is lehet, ahogy arról a biztonság kapcsán volt is szó). Azt se felejtsük, hogy sok eseteben a kimenetek maguk is összetettek: az kevés, hogy "lázgörcs", mert lehet az eset enyhébb és súlyosabb, ez utóbbi tovább megbontható a szerint, hogy jár-e maradandó károsodással vagy sem stb. És persze mindegyikhez külön valószínűségek tartoznak!
Ha mindezeket összegyűjtjük, akkor egész mutatós kis fákat is rajzolhatunk, egy tanulmány például a kanyaró és az ellene védő oltás kapcsán szedte össze a lehetséges kimeneteket, becsült valószínűségeikkel együtt:
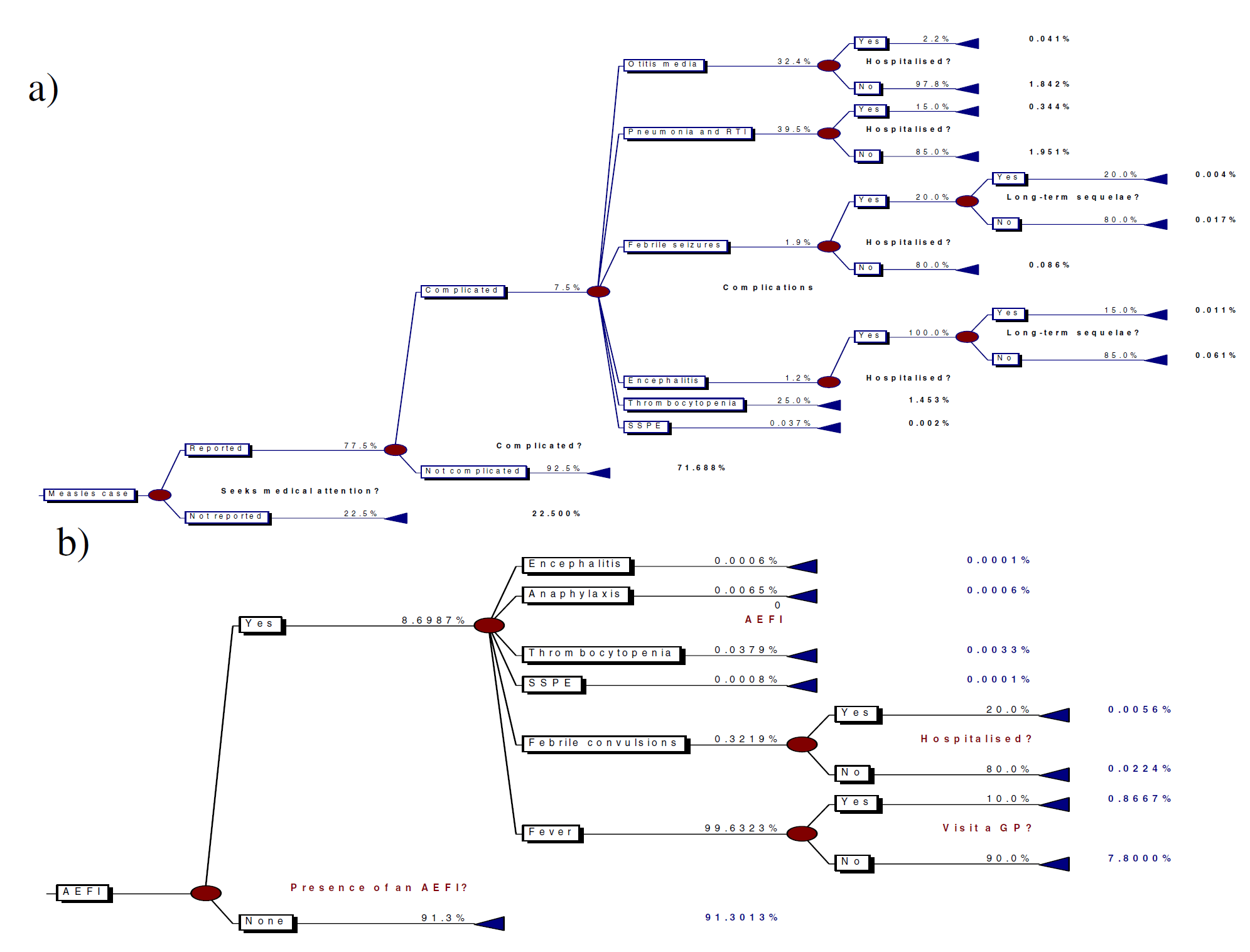
Ha beadjuk a gyógyszert (például védőoltást), akkor a várható történéseknek két komponense van: a gyógyszer mellékhatásai (aminek biztosan kitesszük az alanyt), és a betegség hatásai kezelés mellett. Ez utóbbi természetesen nulla, azaz – egyszerűsítve a helyzetet – figyelmen kívül hagyható, ha a kezelés tökéletes (teljesen megszünteti a betegséget, illetve biztosan megelőzi – függően attól, hogy gyógyító vagy megelőző a kezelés). Ha nem adjuk be a gyógyszert, akkor csak egy komponense van a történéseknek: a kezelés nélküli kimenet. Gyógyító kezelés esetén ez egyszerűen a betegség kezelés nélküli kimenete, de vigyázat, megelőző kezelés esetén nem egyszerűen a megelőzött betegség kimenetei, hiszen tekintetbe kell vennünk annak a valószínűségét is, hogy a nem kezelt – például nem oltott – alany mekkora valószínűséggel kapja meg a kórt. (Újabb sztochasztikus elem!) Amennyiben ez 100%, például a nem oltottak biztosan megbetegednek, akkor ez – újabb egyszerűsítésként – szintén figyelmen kívül hagyható.
Az oltások példájánál maradva, a két egyszerűsítés közül az első nem túl izgalmas: egyrészt könnyen figyelembevehető, mert mindössze annyi a teendő, hogy a gyógyszer mellékhatásaihoz hozzáadjuk a betegség mellékhatásait megszorozva annak a valószínűségével, hogy az alany a kezelés ellenére is elkapja, másrészt a legtöbb kötelező gyermekkori védőoltás hatásossága tényleg igen jó, ezért akkor sem hibázunk túl nagyot, ha ezzel nem is törődünk (a kanyarónál tipikusan így van). A második egyszerűsítés jóval érdekesebb, olyannyira, hogy teljesen külön, a következő alfejezetben foglalkozom ezzel a problémakörrel. De pont a kanyaró a jó példa arra, amikor ez is egy nyugodtan vállalható egyszerűsítés: oltás hiányában tényleg gyakorlatilag mindenki megkapta a kanyarót.
E két feltételezéssel a fenti összehasonlítás tehát két tényező összevetésére redukálódik: a gyógyszer mellékhatásai szemben a betegség lehetséges kimeneteleivel. A kanyaró és a kanyaró ellen védő oltás példáján ezt a következő táblázat mutatja.
|
Szövődmény |
Kanyaró |
MMR-oltás |
|
Láz |
98%, általában magas |
2-10%, ritkán magas |
|
Kiütés |
98% |
5%, csak gyengén |
|
Hasmenés |
5-8% |
1%-0,1% |
|
Középfülgyulladás |
3-7% |
1%-0,1% |
|
Tüdőgyulladás |
1-6% |
nem ismerten kicsi |
|
Lázgörcs |
0,1-2% |
1/1000 – 1/3000 |
|
Trombocitopénia |
0,1-4% |
1/30 000 – 1/50 000 |
|
Encephalitis |
1/500 – 1/10 000 |
< 1/1 000 000, ha nem nulla |
|
SSPE |
1/50 000 – 1/200 000 |
meghatározhatatlanul kicsi, ha nem nulla |
|
Anafilaxia az oltás valamely összetevőjére |
0 |
< 1/100 000 |
A kockázat-haszon mérleges tehát azt jelenti, hogy e két oszlopot vetjük össze. A dolognak persze nem csak "matematikai" ("melyik szám nagyobb") szempontjai vannak, hanem pszichológiaiak is – erre még szintén kitérek ebben a fejezetben.
Zárásként még egy dologra hívnám fel a figyelmet. A dolog sztochasztikus jellegéből adódóan egyfajta várható értéket kell vennünk a mérlegelés során, ezért is emlegettem, hogy be kell szorozni a kimenetet annak valószínűségével. A kanyaró esetében szerencsénk volt, mert a betegség kimenetei és az oltás mellékhatásai nagyon hasonlóak, így ezt megspórolhattuk azzal, hogy úgymond soronként vetjük össze a lehetőségeket. (Ahogy pedig már nagyon egyszerű a döntés.) De mi van akkor, ha nincs ilyen szerencsénk és más jellegűek az összevetendő kimenetek...? Ha a betegség 1% valószínűséggel okoz lázgörcsöt és 5% valószínűséggel hasmenést, míg az oltásnál ugyanez 1 ezrelék és 5 ezrelék (más hatás egyiknél sem lehet), akkor nincsen semmi gond. De mi a helyzet akkor, ha a betegség 1% valószínűséggel okoz lázgörcsöt (hasmenést nem tud), az oltás pedig 5 ezrelék valószínűséggel hasmenést (lázgörcsöt nem tud)? Ilyenkor hogy döntünk? És ha 1 ezrelék a lázgörcs valószínűsége a betegségnél és 5% a hasmenésé az oltásnál? És ha 1/10 000 a lázgörcs a betegségnél, és 50% a hasmenés az oltásnál...? Gondolom érthető mire akarok kilyukadni: mennyi hasmenés ér (!) egy lázgörcsöt? Hogyan lehet egy ilyen kérdésre válaszolni? Mert az tiszta sor, hogy ha 100 embert kiteszünk 1%-os lázgörcs kockázatnak, az várható értékben 1 (ha lázgörcs egységekben számolunk). De ha kitesszük őket 1%-os lázgörcs kockázatnak és még 5%-os hasmenéskockázatnak, annak a várható értéke... mi is?
Az se túl jól megoldás, ha kitaláljuk valahogy, hogy mennyi az átváltás konkrétan a hasmenés és a lázgörcs között. Hiszen akkor feltehetném a kérdést, hogy hány trombocitopénia ér egy tüdőgyulladást, hány középfülgyulladás egy encephalitist... és így tovább. Az egyetlen járható út, ha valahogy megpróbáljuk – ez se könnyű – közös nevezőre hozni ezeket, azaz mindent ugyanarra az alapra átváltani. Egy népszerű megoldás az életév-veszteség használata, de ez is inkább csak akkor jó, ha kizárólag a halálozás a szempont. Erre jó: meg lehet halni hasmenés, lázgörcs és encephalitis szövődményében is, és ha csak erre vagyunk tekintettel, akkor remekül megválaszolható az előbbi kérdés. Ha ezerszer nagyobb lázgörcs szövődményében a halálozás valószínűsége, mint hasmenés szövődményében, akkor 1000 hasmenés ér 1 lázgörcsöt. És hasonlóan összehasonlítható válik az encephalitis, és minden más is.
A probléma, hogy az orvosi gyakorlatban nem lehet ennyire halálozás-orientáltnak lenni, nem tehetjük ezt kizárólagos célfüggvénnyé. Például a lázgörcsnek lehet maradandó neurológiai szövődménye, az nem is számít? (Az életév-veszteségben nem!) Akkor tehát, ha az egyik lehetőség, hogy 100% valószínűséggel kognitív deficit lép fel, de halál nélkül, míg a másik, hogy minden egymilliomodik alany meghal, de a többinek kutya baja, akkor az előbbit kell preferálnunk...? Az életév-veszteség metrika szerint igen!
Egy tipikus megoldás ennek kezelésére, hogy szakítunk a bináris szemlélettel (halál: számít, bármi más: nem történt semmi), és ezt egy folytonosabb skálává tesszük, figyelembe véve valamiféle életminőség-mutatót. Például azt mondjuk, hogy a halál esetén a további életminőség 0, de kognitív deficit esetén sem 1 – mint eddig – hanem csak mondjuk 0,7. Ez más szóval azt jelenti, hogy ha az alany 50 évet él kognitív deficittel, az egyenértékű azzal, mintha 35 évet él tökéletes egészségben, majd meghal. Persze nagyon is lehet vitatni, hogy az ilyen jellegű összehasonlításoknak van-e egyáltalán értelmük, de tagadhatatlan előnye, hogy legalább kézbentarthatóvá teszi a problémát! A 100%-os valószínűségű kognitív deficit egyenértékű azzal, mintha az alanyok 30%-a meghalna, tehát ha csak minden egymilliomodik hal meg, akkor tényleg az utóbbi a jobb választás – ahogy azt éreztük is. (Az persze egy nagyon jó kérdés, hogy – még ha el is fogadjuk ennek a módszernek a létjogosultságát –, hogyan lehet ezt meghatározni, és olyan kijelentést tenni, hogy "ez a kognitív deficit 87,3%-os életminőséget jelent"...) Ezt hívják minőséggel korrigált életév-veszteségnek (angol rövidítéssel: QALY). Amint az előbbiből is látszik, e módszernek rengeteg kérdőjele, részfeladata és egyéb megközelítése van, itt most ezeket természetesen nem részletezem, pusztán a problémára kívántam felhívni a figyelmet – mert ezt látni viszont fontos.
Eltérő kockázat-haszon mérlegű csoportok egy populáción belül
Az előbbi tárgyalásban, ha jobban meggondoljuk, volt még egy egyszerűsítés: az, hogy egyetlen kockázat-haszon mérlegelést készítettünk, azaz hallgatólagosan elfogadtuk, hogy ez a mérlegelés igaz mindenkire a vizsgált populációban. Sok esetben azonban ez nem helytálló: tipikus, hogy azonosíthatóak emberek olyan csoportjai, akiknél a kockázat-haszon mérlegelés egy vagy több komponense (vagy akár az összes) máshogy viselkedik mint a populáció többi részében. Eltérhet:
- az oltás beadása esetén várt haszon (például bizonyos immunológiailag károsodott emberek, bár inaktivált oltást kaphatnak, de náluk kevésbé fog védőhatást kiváltani mint az immunológiailag egészségeseknél),
- az oltás beadása esetén várt kockázat (például bizonyos immunológiailag károsodott embereknél élő-gyengített ágenst tartalmazó oltás a gyengítés ellenére is súlyos, akár nagyon súlyos betegséget okozhat),
- az oltás be nem adása esetén várt kimenet (mind a betegség elkapásának valószínűsége, mind a lezajlás súlyosságának eltérhet: például gyulladásos bélbetegségben szenvedő nők, különösen ha immunszuppresszív terápiában részesülnek, emelkedett méhnyakrák-kockázattal szembesülnek, a myeloma multiplex-esek pneumococcus kockázata sokkal nagyobb mint az ilyen betegségben nem szenvedőké, hasonlóképpen a pneumococcus – és más tokos baktériumok – okozta fertőzésekre kifejezetten érzékenyebbek az anatómiai vagy funkcionális léphiányban szenvedők, az influenza egy sor krónikus betegségben szenvedő esetén nagyobb kockázatú stb.).
A kérdés értelemszerűen azért fontos, mert ezek az eltérések akár teljesen meg is változtathatják a kockázat-haszon mérlegelést. Hogy mást ne mondjak, a korábban már említett oltási kontraindikációk épp ennek megtestesülései: azért mondjuk – például –, hogy immunológiailag károsodott személyek nem kaphatnak élő ágenst tartalmazó oltást, mert a fenti 2. pont miatt az ő körükben annyira eltér a kockázat-haszon mérleg, hogy már a másik irányba billen. Másik példa lehet a krónikus betegek ösztönzése az influenza elleni oltás beadására, mely a fenti 3. pont következménye.
Sajnos a kérdés azért nehéz ügy, mert sok esetben azt látjuk, hogy betegségek egyszerre növelik az oltás beadásának és az oltás be nem adásának a kockázatát. A védőoltás-ellenesek – meglehetősen visszatetsző módon – előszeretettel hivatkoznak ilyenkor arra, hogy micsoda veszélyeztetés, hogy még a beteg gyereket is így meg úgy oltják, ám ez figyelmen kívül hagyja, hogy épp ezek a gyerekek azok, akiket a fertőző betegségekkel szembeni védetlenül hagyás is a legjobban veszélyeztet! Az egyszerűség kedvéért elfogadom látatlanban, hogy egy myeloma multiplex-es beteget kockázatosabb beoltani pneumococcus ellen, mint egy egészségeset – csakhogy egy ilyen betegnek az is sokkal kockázatosabb, ha nincs beoltva. (Néha már az az ember érzése, hogy legfeljebb a makkegészséges embereket oltanák be – ha egyáltalán... –, azaz épp azokat oltanák, akinek a legkevésbé van rá szüksége, és azokat nem, akiknek a leginkább.) Arra meg a visszatetsző is nagyon enyhe kifejezés, amikor egy külföldi hírre, miszerint egy gyermek meghalt kanyaróban, úgy reagálnak, hogy "jó, persze, de ő eleve beteg volt" – miközben két oldallal odébb azt harsogják, hogy az eleve betegek azok, akiket aztán végképp semmiképp nem kellene beoltani!
Ritka betegségek megelőzése: az abszolút és a relatív kockázat
Az az egyszerűsítés, hogy a nem oltás kockázataként a betegség kockázatát tüntettük fel, csak akkor fogadható el, ha az oltatlanok biztosan megbetegednek a kórban. Ez kanyaró esetén rendben van (különösen, ha nem egy ember be nem oltásáról beszélünk, hanem általában a kanyaró elleni oltás nem alkalmazásáról), de más betegségek esetén bonyolultabb a helyzet: a védőoltás bevezetése előtti érában sem lett diftériás mindenki!
Azért mondtam, hogy ez bonyolultabb helyzet, mert ha érdemi valószínűsége van annak, hogy a betegséget el sem kapja az ember, akkor a kockázat-haszon mérlegelés bonyolódik, hiszen ezt az eshetőséget is tekintetbe kell venni: a haszon csökken, ha oltás nélkül sem biztos, hogy bajom lesz. Ha a betegségtől minden tizedik embernek hasmenése lesz, de a betegséget oltatlanul is csak 10% eséllyel kapom el, akkor az oltatlanságból fakadó hasmenés kockázatom csak 1%, nem 10! (100 emberből, hiába is oltatlanok, csak 10 fog megbetegedni, 10 megbetegedettből 1-nek lesz hasmenése – a kockázat tehát 1/100=1%.) Ez a kérdéskör különösen éles lehet ritka betegségek esetén.
Ennek kapcsán számos félreértéssel találkozni, aminek talán legfontosabb oka, hogy sokak számára nem világos az abszolút kockázat(különbség) és a relatív kockázat(arány) közti fogalmi eltérés. Hadd illusztráljam ezt egy konkrét, és témába vágó példán. A BCG vakcina jó hatásfokkal véd a gyermekkori TBC-s meningitis, azaz agyhártyagyulladás ellen; a kerekség kedvéért mondjuk, hogy az oltás hatásossága ez ellen 75%. Magyarországon elvétve fordul elő ilyen eset, az egyszerűség kedvéért kerekítsünk felfelé, és mondjuk, hogy évente 1 az esetszám a 0-14 éves korosztályban. Feltételezve, hogy hazánkban mindenki részesült BCG-ben, ami elég jó közelítés, ez azt jelenti, hogy oltás híján 4 esetre kellene (kellett volna) számítanunk. Mivel e korosztály létszáma kb. 1,5 millió, így az oltás nélküli kockázat a korcsoport egészében nagyjából 2,7/év/millió fő lenne, oltással 0,7/év/millió fő. (Annak a kockázata, hogy egy újszülött a 14 éves kor eléréséig valamikor megbetegszik, természetesen jóval nagyobb, hiszen e kockázatot kell sok éven keresztül kumulálni, de ezzel most nem törődöm, hogy a példát egyszerűen tartsam; az esetek nagy része amúgy is az első néhány évre koncentrálódik.)
Ez azt jelenti, hogy a BCG-vel oltottak relatív kockázata lényegesen kisebb, mint az oltatlanoké: nagyjából egynegyede. Persze, ez épp az oltás hatásossága – ez teljesen rendben is van, az oltás jóságát magát tényleg ez a (relatív) érték jellemzi. Csakhogy mindeközben az abszolút kockázatkülönbség oltottak és oltatlanok között még így is roppant kicsiny: mindössze 2/év/millió fő! Ez persze nem az oltás hibája, sőt, ennek semmi köze az oltáshoz: ez annak a "hibája", hogy e betegség kockázata még az oltatlan csoportban is nagyon alacsony. Az abszolút kockázatkülönbség a gyógyszer jóságából (a relatív kockázatból) és az oltás nélküli kockázatból – szokták úgy is mondani: a baseline rizikóból – tevődik össze. Az előbbiről "tehet" az oltás, az utóbbi a betegség adott népességbeli elterjedtségén múlik.
Hogy ez miért lényeges? Azért, mert bár első ránézésre mondhatjuk, hogy az oltás évente 3 gyermeket ment meg ettől az – egyébként borzasztó, és igen rossz prognózisú – betegségtől, valójában azonban kicsit bonyolultabb a kép. Igaz, hogy a 1,5 millió gyermekből évente 3 specifikusan az oltás miatt nem lesz TB meningitis-es (az esetükben nyilván egy pillanatig nem kérdés, hogy az oltást megérte beadni), viszont 1 499 996-ot feleslegesen oltunk be (mert oltás nélkül sem betegedne meg), 1-et pedig hiába oltunk be (mert az oltás ellenére is meg fog betegedni) – csakhogy az oltás mellékhatásainak őket is kitesszük! Az oltás jól működik, nem ezzel van a probléma (relatív értelemben tényleg jó), csak a megelőzendő betegség ritka. Furcsa lehet a "75%-os a hatásossága!" és a "1,5 millió emberből 3-nak tesz jót!", pedig csak szorozni kell tudni, hogy lássuk: ebben az esetben ez a kettő ugyanaz! Ami azért is probléma, mert hiába ugyanaz, az emberek – nem meglepő módon – teljesen másképp érzékelik a kettőt; ha egy gyógyszer jóságát abszolút valamint relatív módon adjuk meg, akkor nagyon sokan ellentétes döntésre jutnak a használatáról, pusztán a közlési formától függően, miközben az információ pontosan ugyanaz.
Érdemes megfigyelni az univerzális oltási stratégiát: a 1,5 milliós szám azért olyan nagy, mert meg sem próbáljuk megkeresni a kockázatnak kitett, rizikócsoportbeli alanyokat, hogy csak őket oltsuk célirányosan. (Persze lehet, hogy azért nem próbáljuk, mert nem is tudjuk. Ez lenne a szelektív stratégia, aminek az alkalmazhatósága – többek között – azon múlik, hogy van-e jól körülhatárolható rizikócsoport, ahol tényleg nagy fokban koncentrálódnak a későbbi megbetegedők, és kivitelezhető-e az ő célirányos oltásuk. Ez persze komoly kérdés lehet a gyakorlatban, de ha pozitív a válasz, akkor az sokat tud javítani a fenti arányokon.)
Mindennek egy szemléletes, és jól értelmezhető mérőszámát kapjuk, ha kiszámítjuk, hogy hány embert kell beoltani ahhoz, hogy megelőzzünk egy megbetegedést. Könnyű észrevenni, és az előző bekezdés végének számításából is látható, hogy ez nem más, mint az abszolút kockázatkülönbség reciproka; példámban \(\frac{1}{2,7-0,7}=500\) ezer fő. Ennyit kell beoltani ahhoz, hogy egynek megelőzzük a megbetegedését. Megjegyzem, hogy ez a mutató nem más, mint az orvoslás más területein jól ismert ’number needed to treat’ mérőszám alkalmazása védőoltásokra; szokás néha ezt a number needed to vaccinate (NNV) névvel is illetni. Világos a fenti levezetésből, hogy az NNV nem csak a védőoltás hatásosságától függ (ami a relatív kockázatot határozza meg), hanem a betegség incindenciájától is (ami "átváltja" a relatív kockázatot abszolútra). Pontosan ez az oka annak is, hogy a nemzetközi ajánlások is a TBC-vel való fertőződés kockázatától teszik függővé azt, hogy az univerzális vagy a szelektív BCG-oltási stratégia célravezetőbb-e egy országban.
Hiába igaz tehát, hogy az oltás mellékhatás-kockázata elhanyagolható a TBC-s meningitis "mellékhatás"-kockázata mellett, valójában nem ezt a kettőt kell egybevetni: a korrekt összehasonlítás az, ha a BCG mellékhatás-kockázatát 500 ezerrel (!) felszorozzuk, és ezt hasonlítjuk a TBC-s meningitis kockázatához! Ez a különbség az előbbi táblázathoz képest: itt nem a két oszlopot kell egymáshoz hasonlítani, hanem az egyik oszlop 500 ezerszeresét a másikhoz! Az nem kérdés, hogy a BCG mellékhatásainak kockázata elhanyagolható a TB meningitishez képest, de hogy az 500 ezerszeresük is elhanyagolható-e, az már egyáltalán nem nyilvánvaló.
Az összehasonlítás tényleges elvégzését itt is ugyanúgy komplikálja az a kérdés, hogy milyen módon lehet teljesen különböző jellegű eseményeket összevetni. Példának okáért, ha a BCG lymphadenitis kockázatát kereken 2 per 10 ezernek vesszük, akkor az 500 ezerrel való beszorzás után azzal a kérdéssel szembesülünk, hogy 100 okozott lymphadenitis hogyan viszonyul 1 megelőzött TBC-s meningitis...? (A pontos összehasonlításban persze a lymphadenitis mellett fel kell sorolni a többi mellékhatást, és hasonlóan a TB meningitis mellett a többi megelőzött betegséget; természetesen valószínűségeikkel együtt.)
Ami világosan látszik a fentiekből, hogy miért igaz az az alaptétel, hogy ritka betegség ellen csak rendkívül biztonságos vakcinával szabad oltani!
Végezetül a fenti – nyilván csak illusztratív – példa után nézzünk meg egy konkrét, pontosan végigszámolt gyakorlati alkalmazást! Lim és mtsai azt vizsgálták egy kanadai tartomány példáján, hogy mennyire működőképes stratégia az újszülöttek védelme a szamárköhögéstől a velük érintkező szülők, testvérek stb. beoltása révén. ("Cocooning" stratégia, avagy fészekimmunizálás – én is érintettem a nyájimmunitás kapcsán.) Eredményül azt kapták, hogy egy eset megelőzésére az NNV 500 és 6400 közötti (függően attól, hogy pontosan mennyi a betegség előfordulása, illetve, hogy mit feltételezünk arról, hogy a gyermekek mekkora része kapja meg a betegséget a szüleitől), egy hospitalizáció megelőzésére 12 000 és 63 ezer közötti, egy halálozás megelőzésére 1,1 és 12,8 millió (!) közötti. (Gondoljuk végig, hogy miért nőnek ezek a számok: minél ritkább a végpont, amit vizsgálunk, annál kisebb lesz az oltás nélküli – baseline – kockázat is.) Ez egyáltalán nem hangzik bíztatóan, sőt, de azért azt se felejtsük el, hogy ez csak a mérleg egyik oldala: meg kell vizsgálnunk az oltás mellékhatásait is – ha azok rendkívül csekélyek, akkor akár nagy NNV is megérheti. Mindemellett persze ezek az adatok nem vihetőek át gondolkodás nélkül más országokra, hiszen függenek attól, hogy az adott viszonyok között milyen a pertussis előfordulása.
A kockázat érzékelése, kommunikációja
Amit eddig láttunk, az a "vegytiszta matematika" volt. A valóságban azonban az emberek nem matematikai alapon döntenek, a kérdés nem csak azon múlik, hogy két szám közül melyik a nagyobb, hanem az egyéni beállítódásaink, előzetes tapasztalataink, értékeink és egy sor érdekes pszichológiai mechanizmus befolyásolja. Kihat arra, hogy hogyan érzékeljük a kockázatokat és hogy hogyan hasonlítjuk össze azokat. Mindezeknek természetesen nagyon komoly kihatása van arra, hogy hogyan érdemes kommunikálni a kockázatokat. E kérdés jórészt inkább pszichológiai, szociológiai, úgyhogy itt részletesen nem foglalkozom vele (de a megfelelő irodalmakra mindenhol utalok), inkább csak kiemelem a talán legfontosabb eredményeket.
Ami a kockázatok érzékelését illeti, ha egy mondatban kellene összefoglalni az ezzel kapcsolatos legfontosabb megállapításokat, akkor az így hangozhatna: kockázatok érzékelésében nagyon rosszak vagyunk. Hajlamosak vagyunk a kis kockázatokat fölébecsülni, a nagyokat alá, különösen rosszul érzékeljük a különbségeket a nagyon kis számok világában, elfogultak vagyunk bizonyos nevezetes küszöbértékek iránt (például pontosan nulla kockázat), de ami a legfontosabb: a kockázatokat nem önmagukban – mint számokat – értékeljük, hanem a jellegüket is figyelembe vesszük. Empirikus pszichológiai kísérletek igazolták, hogy sokkal nagyobbnak érzékeljük azokat a kockázatokat
- amelyeket ránk kényszerítenek, szemben azokkal, amiket amiket önként vállalunk,
- amelyek tudatos emberi tevékenység eredményei, szemben azokkal, amik természetes történés következményei (másként megfogalmazva: amiket tudunk irányítani, szemben azokkal, amiket nem),
- amelyek jellegét nem értjük jól, nem ismerjük, szemben azokkal, amiket értünk, megszoktunk,
- amelyek ijesztő, vagy rettegett következményekkel járnak, szemben azokkal, amik következményei hétköznapibbak,
- amelyek egyéniek, szemben azzal, amik anonim tömegekre vonatkozó "statisztikák".
Fontos világosan elválasztani egymástól a kockázat érzékelését és elfogadását. Az, hogy egy kockázatot mikor tartunk elfogadhatónak, egy külön kérdéskör, mert attól is függ, hogy mik az – érzékelt – előnyei; itt tehát már a mérlegelés is szerepet fog játszani – természetesen szintén számos szubjektív elemmel, melyről komoly viták folytak az elmúlt évtizedekben. Ami ezekből kiemelendő, hogy a kockázat alacsony volta önmagában nem jelenti azt, hogy elfogadhatóvá válik, valamint, hogy a mérlegelés többszempontú, gyakran kvalitatív elemeket is tartalmaz, így jellemzően nem redukálható egyetlen számra (pl. halálozási valószínűségre), amit aztán össze lehet egyszerűen hasonlítani.
Ez pedig már átvezet minket az utolsó kérdéskörre: a kockázatok kommunikációjához. Ennek milliónyi aspektusa van ami a védőoltások szempontjából is releváns, én most egyet emelnék ki: a védőoltások jelentette kockázat olyan kommunikációját, ami ezeket teljesen más kockázatokhoz hasonlítja. Jó ötlet-e olyat mondani, hogy "anyuka, annak, hogy most beadom a védőoltást, kisebb a kockázata, mint az autóbaleset veszélyéből fakadó kockázata annak, hogy eljöttek ide"? Mivel ez tényleg így van, nagyon csábítónak tűnhet a dolog – olyan értelemben, hogy ez biztos nagyon meggyőző – és hosszú időn keresztül csakugyan egyértelműen jó stratégiának tartották ezt, ám a '80-as években vált világossá, hogy ez nem biztos, hogy annyira jó ötlet. A probléma következik az előző bekezdésekből: ez a stratégia figyelmen kívül hagyja, hogy az emberek hogyan érzékelik a kockázatokat. Specifikusabban: figyelmen kívül hagyja, hogy a kockázat érzékelésében nem csak a számszerű nagysága játszik szerepet, hanem egy sor egyéb tényező is, például az önként vállaltsága. Az autóvezetés önként vállalt kockázat, a kötelező védőoltás beadása nem. Ez egy kritikus elem abban, hogy az emberek hogyan érzékelik a kockázatokat, a figyelmen kívül hagyása "almát hasonlítunk a körtéhez" helyzethez vezethet: az igaz, hogy a kockázat nagysága ugyanaz, de a fenti mondat azt sugallja, hogy akkor az elfogadása is azonos kell legyen – ami viszont nem igaz! Ez empirikus pszichológiai tény. A másik probléma, hogy az ilyen összehasonlítások figyelmen kívül hagyják az emberek rizikó-érzékelésének azt az aspektusát, hogy az többszempontú (azáltal, hogy egyetlen számra redukálják azt, amiben az összehasonlítást teszik). És mindezeken felül azt sem fejezik ki, hogy ezekben a kockázatokban bizonytalanságok vannak, pontosan nem ismert az értékük, ami ismét csak a hiteltelenedés irányában hat. Ráadásul nem csak arról van szó, hogy mindezek miatt ez nem helytálló ilyen formában, de sok embert elidegeníthet, sőt, feldühíthet egy ilyen összehasonlítás, különösen ha vita-helyzetben hangzik el, vagy nincs nagyfokú bizalom a felek között, így nem csak az a probléma, hogy nem működik jól, de adott esetben kifejezetten visszaüthet. Bár van ennek kapcsán vita, de a legtöbb szakértő emiatt azt javasolja, hogy az ilyen összehasonlításokat kerülni kell, vagy legalábbis arra kihegyezni, hogy a célunk a kockázat nagyságának érzékeltetése, kontextusba helyezése, nem az elfogadhatóságának megteremtése.
Pontosan emiatt csak óvatos felhasználásra, de a korábbi táblázat izgalmasabb – kisebb valószínűségű, azaz nehezebben érzékelhető – adataiból elkészítettem egy ábrát, hazai viszonyokra adaptálva az összehasonlításokat: felhasználtam a fulladásos és égéses halálozások valamint az autóbalesetek statisztikáit; az előbbiek 2013-ra, az utóbbiak 2012-re vonatkoznak, mindkettő valós, magyar adat. Az ábra jobb oldalán a táblázatban feltüntetett valószínűségeket látjuk néhány kiemelt, ritkább szövődményre. A rögtön mellette lévő vastagon szedett tengely mutatja ennek skáláját (vigyázat, a tengely a közepén meg van törve, hogy a nagyon eltérő valószínűségek is látsszanak: a 35 per millió alattiakat az alsó, a 150 per millió felettieket a felső részről kell leolvasni, a kettő között lévőt kivágtam). A valószínűségi tengely mellett pár ekvivalens skála található, melyeken ugyanazok a valószínűségek láthatóak, de átszámítva ekvivalens expozícióra. (Tehát például 32,3 hónap alatt 28 per millió valakinek a kockázata arra, hogy meghal tűz vagy láng okozta égés következtében.) Az égés és a fulladás esetében az expozíciót egyszerűen az életben eltöltött idővel mértük – ez jelenti a "kockázatban levést" ezeknél a veszélyforrásoknál –, az autóbaleseteknél reálisabb módon a megtett kilométerek száma az expozíció a kockázatnak. Mivel a kockázatok nem biztosan ismertek – ahogy azt a táblázat is kifejezi, azzal, hogy sokszor csak intervallumok vannak megadva – ez az ábra is visszaadja ilyen esetekben a bizonytalanságot azáltal, hogy nem konkrét számok, hanem az egész intervallumok jelennek meg (a "doboz" alsó széle a legkisebb, a felső a legnagyobb becsült gyakoriság); ennek fontosságáról már volt szó.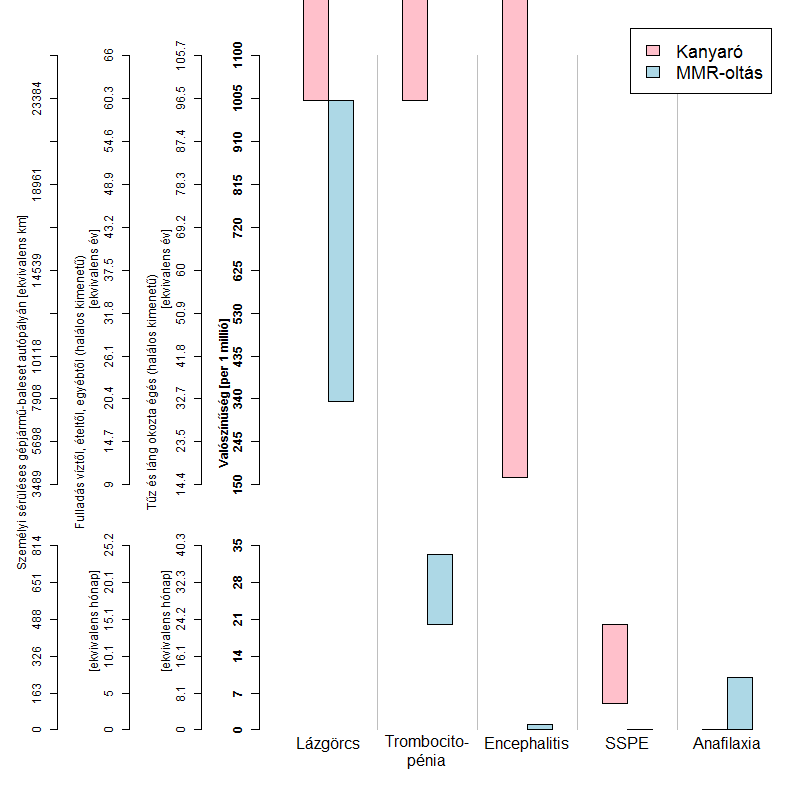 Mi ezen adatok helyes használata? Az egyik fontos szempont, amire tekintettel kell lennünk tehát az, hogy ezeket az összehasonlításokat, ha használjuk is, inkább arra használjuk, hogy a nagyságrendet érzékeltessük, ne olyan értelemben, mint ami önmagában elfogadhatóvá teszi az oltás kockázatát. A másik rendkívül fontos gondolat, hogy az viszont egy sokkal helytállóbb összehasonlítás, ha az oltás beadásának a kockázatát az oltás be nem adásának a kockázatához hasonlítjuk. Erről korábban már részletesen volt szó, itt csak azt ismételném meg, hogy érdemes hangsúlyozni: pont a kanyaró kapcsán tényleg e kettő között kell választani, más lehetőség nincs! Pontosan azért, hogy az ábra ezt is támogassa, feltüntettem rajta nem csak az oltás, de a természetes kanyaró kockázatait is, ugyanolyan skálázással, összehasonlíthatóan.
Mi ezen adatok helyes használata? Az egyik fontos szempont, amire tekintettel kell lennünk tehát az, hogy ezeket az összehasonlításokat, ha használjuk is, inkább arra használjuk, hogy a nagyságrendet érzékeltessük, ne olyan értelemben, mint ami önmagában elfogadhatóvá teszi az oltás kockázatát. A másik rendkívül fontos gondolat, hogy az viszont egy sokkal helytállóbb összehasonlítás, ha az oltás beadásának a kockázatát az oltás be nem adásának a kockázatához hasonlítjuk. Erről korábban már részletesen volt szó, itt csak azt ismételném meg, hogy érdemes hangsúlyozni: pont a kanyaró kapcsán tényleg e kettő között kell választani, más lehetőség nincs! Pontosan azért, hogy az ábra ezt is támogassa, feltüntettem rajta nem csak az oltás, de a természetes kanyaró kockázatait is, ugyanolyan skálázással, összehasonlíthatóan.


