Miért oltunk, avagy mire jók a védőoltások? Sokan erre a kérdésre azt válaszolnák: azért, hogy megelőzzük a beoltott személy megbetegedését. Ez persze igaz, de valójában többről is szó van.
Ezen írás kulcsüzenetei:
- Egy személy nem csak a szó hagyományos ("immunológiai") értelmében lehet védett egy betegség ellen: akkor sem tudok megbetegedni, ha ugyan nem vagyok védett, ám mindenki akivel érintkezem, az – és így nincs kitől elkapnom a betegséget.
- Ha egy populációban elég nagy arányban védettek az emberek, és a védetlenek egyenletesen oszlanak el közöttük, akkor előállhat az a helyzet, hogy minden védetlen a fenti helyzetben van: csupa védettel érintkezik. Ilyenkor hiába is betegszik meg egy védetlen, nem fog járvány kitörni, hiszen nem tudja kinek átadni a betegséget.
- Mindez azt jelenti, hogy hiába nem 100% a védettek aránya, a populációnak mégis 100%-a védett. Más szóval: a védettek védelme kiterjed a védetlenekre is, egyfajta indirekt védelmet kapnak ők is. Ezt hívjuk közösségi (vagy nyáj-) immunitásnak.
- Amennyiben a védettség meghatározó módon az oltásból származik (ez egy sor fertőző betegségre igaz modern körülmények között), akkor a fentiek azt jelentik, hogy ha a populáció elég nagy részét be tudjuk oltani, akkor nem csak az oltottakat magukat tudjuk megvédeni, hanem azokat is, akik nem kaptak oltást, vagy kaptak, de nem váltotta ki náluk a védőhatást. Hogy mennyi a szükséges átoltottság, az epidemiológiai modellekkel jól meghatározható.
- Mindez fordítva elmondva: ha ezen átoltottság alá esünk, akkor ki tudnak törni járványok, és így hirtelen mindenki veszélybe kerül: akik túl fiatalok az oltáshoz, akiknél betegségük miatt nem vált ki védettséget az oltás, várandósok stb. Az oltás beadására vonatkozó döntés tehát nem tisztán egyéni döntés, hiszen a közösségét egészét (is) befolyásolja.
- Az írás részletesen bemutatja a fenti jelenséget, ismerteti az említett epidemiológiai modellek alapjait, és számos egyéb következményét áttekinti annak, hogy a védettségnek nem csak egyéni, hanem társadalmi hatásai is vannak (pl. oltási programok esetleges paradox hatása).
A védőoltások közvetlen célja természetesen tényleg az, hogy a beoltott személyt megvédjük valamilyen betegségtől. A védőoltások lényegében egy módszert jelentenek, hogy egy személy immunrendszerét kitegyük egy kórokozónak, de irányított időzítéssel és kontrolláltan, azaz az eredeti betegséget okozni nem képes – legyengített vagy nem is élő – kórokozónak, vagy egy komponensének, mely emiatt a betegség kockázatai nélkül éri el, hogy az immunrendszer megtanulja a kórokozóra történő válaszadást, és ilyen módon a későbbiekben már védett legyen az igazi betegséggel szemben is.
A védőoltás beadása után a legtöbb ember immunrendszere átmegy azon a tanulási folyamaton, amelyen a természetes fertőződés esetén is átmenne – csak éppen a klinikai megbetegedés kockázatai nélkül. (Sok esetben az is elmondható, hogy a betegséggel amúgy is biztosan vagy valószínűen találkozna a szervezet, annak minden kockázatával, például a kanyarót lényegében a gyermekek 100%-a megkapta a védőoltás bevezetése előtt.) A "legtöbb" persze nem azonos a mindenkivel, kifejezve azt, hogy egyetlen védőoltás – mint ahogy egyetlen más megelőzési módszer – sem tökéletes. Ezt hívják primer hatástalanságnak, ez az egyik forrása a védőoltások nem tökéletes hatásosságának.
Ezen tanulási folyamat után a beoltott személy – mivel az immunrendszere már "edzett" – hosszabb-rövidebb ideig védett lesz a betegség ellen. Érdekes kérdés, hogy mit jelent a "hosszabb-rövidebb ideig". Bizonyos oltásoknál (pl. az MMR-nél) ez rendkívül hosszú idő – az MMR kanyaró-komponensénél például olyan hosszú, hogy még 20-30 év távlatában sem volt érdemi gyengülés kimérhető és azokban az országokban, ahol régóta és széles körben oltanak, még 50 év kanyaró nélkül, csak oltás adta védelemben eltelt időszak után sem tapasztalható, hogy a kanyaró érdemi mértékben visszajönne. Más oltások esetében nagyon is belátható ez az időtartam – ma már egyértelmű javaslat például, hogy DTP-oltásból a felnőttek is adassanak be maguknak, egyáltalán nem sűrűn, 10 évente bőven elég, de ennyi időnként oltassák be magukat, hogy frissítsék a védelmüket, elsősorban a szamárköhögés ellen ("emlékeztető" oltás). Az oltás adta védelem ilyen, időbeli gyengüléssel kialakuló elégtelenségét hívják szekunder hatástalanságnak. Ez a másik forrása a védőoltások tökéletlenségének.
Összefoglalva, a védőoltások nem védik meg tökéletesen a lakosságot. Nemcsak arról van szó, hogy nem lehet mindenkit beoltani (nem tökéletes átoltottság), hanem arról is, hogy a beoltottak sem válnak védetté mindahányan (primer hatástalanság), sőt, aki az oltás után védetté vált, annak is csökkenhet idővel a védettsége (szekunder hatástalanság).
Akkor tehát, ha a lakosság védettsége mondjuk összességében csak 90%, az azt jelenti, hogy 10% eséllyel megkaphatom a betegséget? A válasz az, hogy nem!
A helyzet ugyanis a valóságban jobb. Képzeljük el, hogy egy 10 milliós országban 9 999 999 embernek 100%-os a védettsége, 1 emberé pedig 0%-os. Ekkor mennyi a védettség társadalmi szinten? Ellentétben azzal, amit elsőre gondolnánk, hogy ti. 9 999 999 / 10 000 000 = 99,99999%, valójában nem: a védettség ugyanúgy 100% lesz, mintha mindenki tökéletesen védett lenne – hiszen nincs, akitől az az 1 ember megkaphatná a betegséget! Azaz valaki nem csak a szó szoros (immunológiai) értelmében lehet védett, hanem a közösségi viszonyai révén is, azáltal, hogy nem érintkezik olyannal, aki védtelen lenne. Ezt a jelenséget, tehát azt, hogy valaki azért védett, mert bár immunológiailag nem védett, de nincs akitől megkapja a betegséget, hívjuk közösségi (vagy nyáj-) immunitásnak. Úgy is szokták mondani, hogy a védett személyek védelme "kiterjed" a többiekre is, ezért ők egyfajta indirekt védelemben részesülnek (a direkte védettek révén).
A valóságban nyugodtan lehet 10, 100 vagy akár 1000 nem védett ember is, az össztársadalmi védettség, szemben az egyénivel, továbbra is 100% lesz, hiszen a nem védettek várhatóan olyan messze lesznek egymástól, hogy nem tudják egymásnak átadni a betegséget, azaz a körülöttük lévő csupa védett őket is ugyanúgy megvédi, mintha maguk is (immunológiailag) védettek volnának. Járvány nem tud kitörni, hiába nem tökéletes egyéni szinten a védelem.
De vajon hol van pontosan ez a határ? Meddig mehet le a fogékonyak aránya – és ebből adódóan: meddig mehet le az átoltottság –, hogy a nyájimmunitás érvényesüljön és ne tudjanak járványok kitörni? A kulcs e kérdés megválaszolásához, hogy a járvány attól járvány, hogy önfenntartó. Mikor lesz egy betegség terjedése önfenntartó? Akkor, ha minden beteg átlagban több mint 1 embert betegít meg. Ha 1 beteg átlagban 2 másiknak adja át a fertőzést (szép szóval: ennyi másodlagos fertőzést generál), akkor járvány fog kitörni. A lényegen nem változtat, ha 1,1-nek vagy 10-nek, csak a járvány kirobbanásának a sebessége fog eltérni. (Hogyan tud 1,1 ember megbetegedni? Úgy, hogy ez egy átlag. Gondolhatunk rá úgy, hogy 10 beteg ember összesen 11 másikat betegített meg.) Ezt az értéket szokás effektív reprodukciós számnak nevezni; a járvány kitörését tehát az dönti el, hogy ez kisebb vagy nagyobb-e 1-nél. Azaz ahhoz, hogy megválaszoljuk a feltett kérdést, azt kell megértenünk, hogy az effektív reprodukciós szám értéke mitől függ. E tényezők két csoportra oszthatóak: az effektív reprodukciós szám egyrészt attól függ, hogy a beteg hány másik személyt exponál a betegségnek (hány másikat "kínál meg" a kórokozóval), másrészt attól, hogy az exponáltak közül hányan betegednek meg ténylegesen (hány lesz fogékony).
Az előbbit úgy is meg szokták fogalmazni, hogy ha egy fertőzöttet bedobunk csupa tökéletesen fogékony ember közé, akkor várhatóan hány másodlagos fertőzés jön létre. Az ezt befolyásoló tényezők ismét csak két csoportra oszthatóak. Az ugyanis, hogy egy beteg hány másik embert tesz ki a megbetegedésnek, függ egyrészt a kórokozó biológiai jellemzőitől: a kanyaró például cseppfertőzéssel terjed és minimális érintkezés, akár csak rövid idejű egy légtérben tartózkodás is elég ahhoz, hogy a vírus átugorjon az egyik emberről a másikra, így itt magas lesz ez a szám, addig a HIV szexuális érintkezéssel terjed, így ott alacsonyabb (hiszen a szexuális érintkezés feltételezi az egy légtérben tartózkodást, de ez fordítva nem igaz). Természetesen számít az is, hogy egy beteg ember milyen hosszú időtartamon át fertőző, ami ismét csak biológiai kérdés, például a kanyarónál ez az időtartam egy-két hét körüli, HIV-nél a körülményektől függően ennek sokszorosa is lehet – ha ez az érték nagyobb, az szintén növeli az exponált emberek várható számát. A tényezők másik csoportja nem biológiai, hanem társadalmi, hiszen ilyenek is befolyásolják, hogy milyen sűrűn alakul ki az emberek között fertőzés átadására alkalmas kapcsolat: az is számít, hogy milyenek a szociális viszonyok, például a lakókörülmények, a zsúfoltság (ez azonnal világos a kanyaró példáján: ez határozza meg, hogy hányakkal leszünk egy légtérben), számíthatnak a higiéniás viszonyok (például a széklettel szennyezett ivóvíz útján terjedő betegségeknél a csatornázás, szennyvíztisztizás), de szexuális úton terjedő betegségeknél természetesen a szexuális szokások is, és így tovább. A végeredményt az ún. elemi reprodukciós számban adjuk meg (jele: \(R_0\)), mely az összes fenti hatást – biológiaiakat és társadalmaiakat egyaránt – összefogva megmutatja azok eredőjét egyetlen számban, tehát, hogy egy beteg átlagosan hány embert tesz ki a fertőzésnek. Látható, hogy ez egy nagyon soktényezős kérdés, és a végeredmény nem becsülhető meg egykönnyen a rendelkezésre álló adatokból, ráadásul a társadalmi tényezők nagyon különbözhetnek különböző időkben és országokban, így általában nem egyetlen konkrét számot adnak meg, hanem egy intervallumot (mely adott betegségre, és adott populációra értendő). A legfontosabb védőoltással megelőzhető fertőző betegségek \(R_0\)-jai napjaink fejlett országaiban jellemző viszonyok mellett az alábbi táblázaton láthatóak:
A legfontosabb védőoltással megelőzhető fertőző betegségek elemi reprodukciós számai (közelítő minimum és maximum fejlett országokban)
| Betegség | \(R_0\) |
| Kanyaró | 12-18 |
| Mumpsz | 4-7 |
| Rubeola | 6-7 |
| Diftéria | 6-7 |
| Szamárköhögés | 12-17 |
| Polio | 5-7 |
| Tetanusz | 0 |
A kanyarós betegek rendkívül sok embert tesznek ki a fertőzésnek: az elemi reprodukciós szám 12-18 körül van napjainkban a fejlett világon. (Ismét hangsúlyozom, hogy ez egy átlag: az is lehet, hogy van olyan kanyarós, aki egyáltalán senkit nem tesz ki a fertőzésnek, és van olyan, aki ötvenet is, de átlagban 12-18 körüli ez az érték.) A mumpsz sokkal visszafogottabb ilyen szempontból, 10 alatti az elemi reprodukciós száma. És végül ott van, félig-meddig szándékos kakukktojásként, a tetanusz: ez a betegség bár fertőző, de nem ragályos (emberről emberre nem terjed) így az elemi reprodukciós száma 0.
Fontos rögzíteni, hogy ezek a tényezők, így az elemi reprodukciós szám, lényegében nem függenek az átoltottságtól, az oltás hatásosságától, a természetes betegségen átesettek arányától stb., tehát általában a védettségtől. Még egyszer: ez csak a "megkínálást" jellemzi, a védettség – ami meghatározza azt, hogy ki betegszik meg ténylegesen – egy élesen elválasztandó, külön tényező.
Menjünk is akkor tovább erre: hányan fognak ténylegesen megbetegedni? Jelöljük a – bármi okból is, de – védettek arányát \(P\)-vel. Ebben az esetben a fertőzésnek kitett \(R_0\) emberből \(R_0\cdot P\) védett lesz, így hiába is az expozíció, nem jön létre másodlagos fertőzés. Az – adott védettségi viszonyok mellett – ténylegesen kialakuló másodlagos fertőzések száma tehát \(R_P=R_0\left(1-P\right)\); ez épp a már bevezetett effektív reprodukciós szám!
Ahhoz tehát, hogy eldöntsük, hogy az effektív reprodukciós szám nagyobb-e 1-nél (és így meghatározzuk, hogy mi a járvány kitörésének a feltétele), a második megértendő kérdés, hogy mitől függ a \(P\) szám, a védettek aránya. Ezt a kérdést ismét érdemes kettéválasztani. Egyrészt a védettségnek vannak, illetve lehetnek természetes okai: az alany korábban már átesett a betegségen, csecsemő és a méhen belüli korban a szervezetébe átkerült anyai antitestek még védik, genetikai vagy egyéb okokból nem fogékony stb. Oltás híján csak ezek a tényezők számítanak, ezek határozzák meg a \(P\)-t. Ha azonban oltással is számolunk, akkor képbe kerül a védettség másik forrása: az oltással indukált immunitással rendelkezők aránya, amit két dolog határoz meg, az átoltottság és az oltás hatásossága. Ezekről még beszélünk később részletesebben, de előtte álljunk meg egy pillanatra, rakjuk össze, hogy most mit tudunk, hol tartunk:
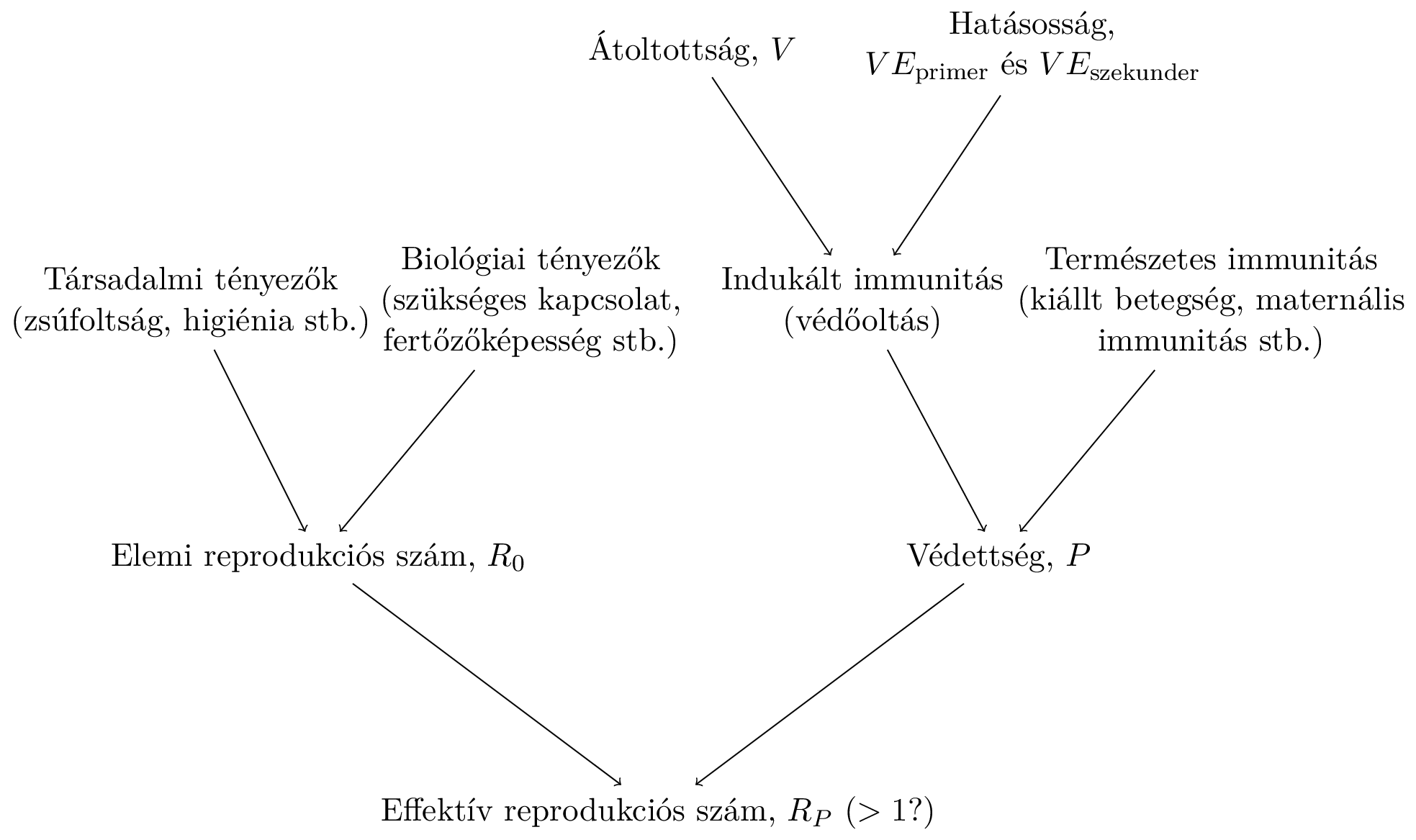
A járványok kitörését meghatározó effektív reprodukciós számot kialakító tényezők
A biológiai és a társadalmi tényezők meghatározzák az \(R_0\)-t. Ez megfelelő módszerekkel megbecsülhető, adott körülmények között adott betegségre jellemző – bár általában nem pontosan ismert – érték. A védettek \(P\) aránya meghatározza az effektív reprodukciós számot: \(R_P=R_0\left(1-P\right)\). Na de mit mondtunk kiinduláskor? Hogy járvány akkor tud kitörni, ha ez a szám nagyobb mint 1! A járvány kitörésének a feltétele tehát:
\[
R_0\left(1-P\right)>1,
\]
amely egyenletet átrendezve azt kapjuk, hogy
\[
P<1-\frac{1}{R_0}.
\]
Megkaptuk tehát, hogy min múlik, kitör-e járvány: akkor fog ez előfordulni, ha a védettek aránya \(1-\frac{1}{R_0}\) alá esik, ahol \(R_0\)-t az adott betegségre és populációra kell meghatározni (a mi viszonyaink között az előbbi táblázat tartalmazza a közelítő értékeit). Például rubeola-járvány nem tud kitörni, ha a populációnak legalább \(1-\frac{1}{6}=83,\!3\)%, \(1-\frac{1}{7}=85,\!7\)% körüli aránya védett.
És itt jön a kulcskérdés: ezek alapján, ha 90% védett rubeola ellen, akkor hiába is van 10% védetlen, ők sem fognak megbetegedni – hiszen ha nem tud járvány kitörni, akkor nem lesz kitől elkapniuk a betegséget! Ez a nyájimmunitás!
Érdemes felhívni rá a figyelmet, hogy az egész okfejtés nem specifikus a védőoltásokra: a nyájimmunitás szempontjából a védettség számít, az mindegy, hogy mi a forrása. Nem véletlen, hogy a bevezető szövegben mindenhol "védett" (és nem "oltott") embereket emlegettem. Ez olyannyira így van, hogy a nyájimmunitás fogalmát már jóval az előtt felismerték, hogy a legtöbb ma használatos védőoltást egyáltalán feltalálták volna. Klasszikus megfigyelés, hogy a védőoltás előtti érában a kanyaró – kb. kétévente ismétlődő – hullámokban jelentkezett, ennek oka is éppen ez: egy nagy kanyaró járvány után megnő \(P\), a védettek aránya (hiszen aki átesett rajta, az már védett lesz), ezért nem tud a betegség újra kitörni. Ez épp a nyájimmunitás egy példája – mindenféle védőoltás nélkül. (Akkor miért tör ki később újra a járvány? Azért mert a megszülető, és anyai védelem alól kikerülő gyermekek visszatöltik a védettség nélküli halmazt.)
Haladjunk most tovább, hogy újabb, gyakorlatban is használható eredményeket nyerjünk. Ehhez először is egy elhanyagolással élünk: a továbbiakban azt feltételezzük, hogy a vizsgált betegségeinkkel szemben nincs természetes immunitás. Igazából nem lenne nehéz ezt is figyelembe venni, de ez anélkül bonyolítaná a számításokat, hogy érdemi változást hozna, ráadásul a közelítés nem rossz, hiszen diftéria vagy mondjuk szamárköhögés ellen tényleg igen jó közelítéssel a mai magyar lakosság 0%-a rendelkezik természetes immunitással, és a kanyaró vagy mumpsz esetén is évről évre esik ez az arány. (Nullára akkor sem fog leesni, ha már mindenki a védőoltások érájában született, hiszen anyai immunitás akkor is marad, ha gyengébb is, mint a természetes betegségen átesett anyáknál, egy-két ember ettől függetlenül is ellenállhat a betegségnek stb. Finomabb elemzéshez ezt is figyelembe kell venni.)
Először tételezzünk fel tökéletes vakcinát, azaz, hogy aki oltott, az védett is. Ez a fenti feltételezéssel együtt azt jelenti, hogy a védettek és az oltottak halmaza egybeesik, azaz \(P=V\), ahol \(V\) az átoltottság. Ebben az esetben tehát az előbbi \(P<1-\frac{1}{R_0}\) kritérium azt jelenti, hogy a feltételünk
\[
V<1-\frac{1}{R_0},
\]
azaz megkaptuk, hogy mi az az átoltottság, ami alatt megszűnik a nyájimmunitás és kitörhetnek járványok. Megfordítva: meg tudjuk határozni, mégpedig számszerűen, hogy milyen minimális átoltottságot kell elérni ahhoz, hogy fennálljon a nyájimmunitás, és ne tudjanak járványok kitörni! A következő táblázat ezt tartalmazza néhány fontos védőoltással megelőzhető fertőző betegségre, az előbbi táblázat folytatásaként.
A legfontosabb védőoltással megelőzhető fertőző betegségek elemi reprodukciós számai (közelítő minimum és maximum a fejlett országokban) és az ezek alapján számolható, nyájimmunitáshoz szükséges minimális átoltottság, tökéletes védőoltás esetén, a természetes immunitást elhanyagolva
| Betegség | \(R_0\) | Szükséges minimális átoltottság |
| Kanyaró | 12 | 91,7% |
| 18 | 94,4% | |
| Mumpsz | 4 | 75,0% |
| 7 | 85,7% | |
| Rubeola | 6 | 83,3% |
| 7 | 85,7% | |
| Diftéria | 6 | 83,3% |
| 7 | 85,7% | |
| Szamárköhögés | 12 | 91,7% |
| 17 | 94,1% | |
| Polio | 5 | 80,0% |
| 7 | 85,7% | |
| Tetanusz | 0 | - |
Jól látszik, hogy – amint az intuitíve is logikus – minél ragályosabb a betegség, annál nagyobb átoltottságra van szükség a nyájimmunitás fenntartásához, és így az oltatlanok indirekt megvédéséhez. Mindazonáltal 95% még a kanyaró legragályosabb feltételezése mellett is elég, 5% oltatlant tehát "elvisel" a rendszer. Rubeola vagy diftéria esetén ennek akár háromszorosát is. Másrészről, tetanusz esetén lehetetlen nyájimmunitást létrehozni – mivel ezt a kórokozót nem másik embertől kapják el a betegek, így az átoltottság, mindegy milyen a mértéke, semmilyen indirekt védelmet nem jelent az oltatlanoknak.
Komolyabb, ún. dinamikus modellekkel, melyekről később még én is fogok szót ejteni, azt is meg lehet határozni, hogy mi történik, ha nem érjük el a fenti küszöböt. Erre mutat példát a következő ábra.
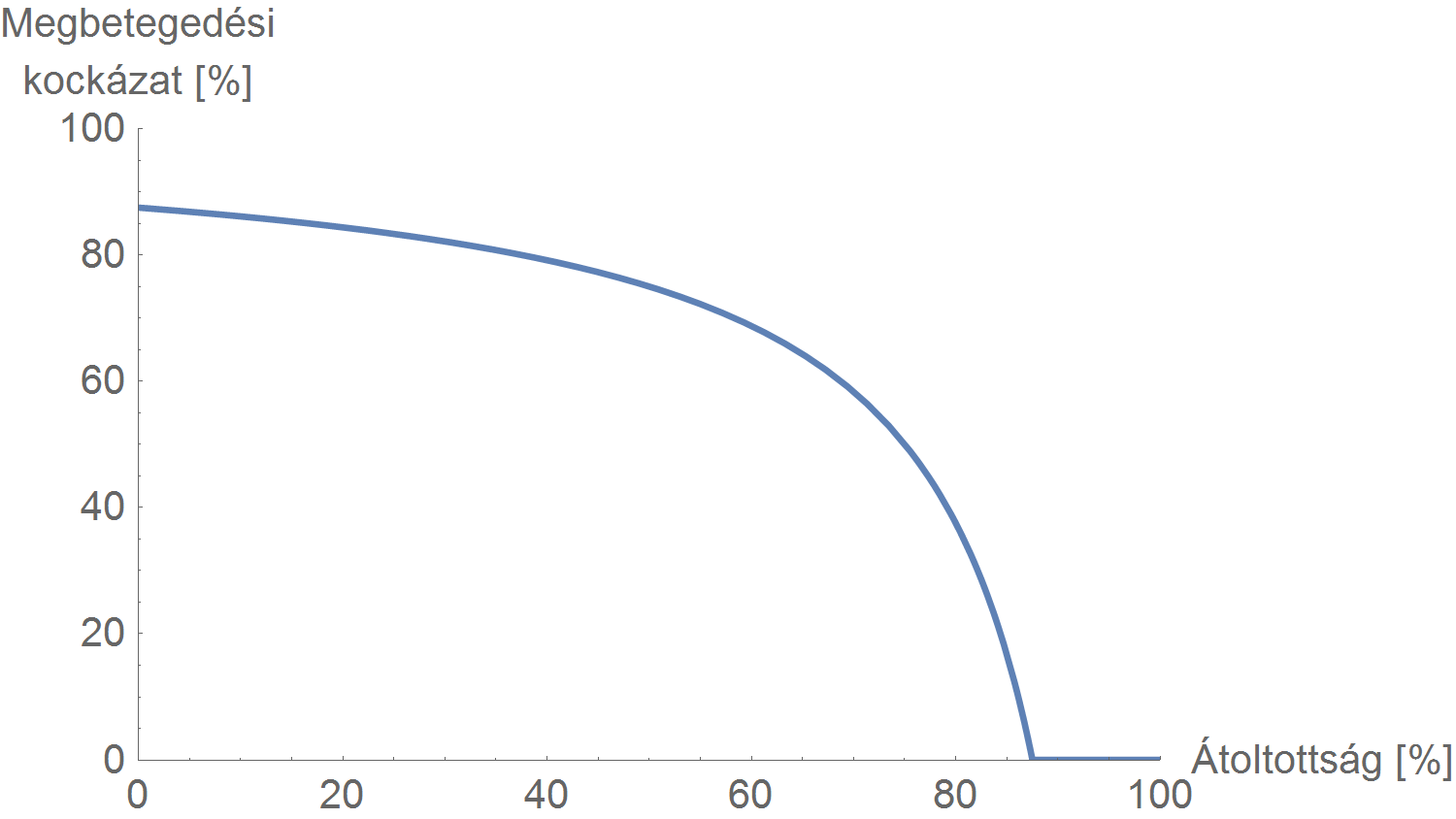
Az oltatlanok megbetegedési kockázata az átoltottság függvényében, egy \(R_0=8\) elemi reprodukciós számú betegség példáján, egyszerű dinamikus modell használatával
Tökéletesen látszik, hogy ha elérjük a kritikus átoltottságot, akkor egzaktan nulla lesz a megbetegedési kockázat – ez az, amit eddig is vizsgáltunk! –, de itt már az is látszik, hogy mi történik, ha oltunk ugyan, de nem érjük el ezt az átoltottságot: csökken az oltatlanok megbetegedési kockázata, hiszen a vírus cirkulációja így is gyengül, de nem nullára. (Ne feledjük: az ábrán természetesen az oltatlanok megbetegedési kockázata látható! Az oltottak kockázata, mivel most még tökéletes vakcinát tételezünk fel, átoltottságtól függetlenül nulla.) Érdemes azt is észrevenni, hogy nulla átoltottságnál sem 100% az oltatlanok kockázata: ősi, bőven védőoltások előtti tapasztalat, hogy még a legnagyobb járványok idején is maradnak emberek, akik annak ellenére sem betegednek meg, hogy fogékonyak lennének a kórra – látható, hogy ez a modell erről is számot ad; ez mellesleg az epidemiológiai modellezés első nagy eredménye volt a XX. század elején.
Közelítsük most a modellünket a valósághoz! Első lépésben vegyük figyelembe, hogy a védőoltások nem tökéletesen hatásosak. A tökéletlenség modellezését kezdjük a primer értelmű tökéletlenséggel: nem mindenki válik védetté, akit beoltanak. Ha a vakcina – primer értelmű – hatásosságát \(VE_{\textrm{primer}}\)-rel jelöljük, akkor \(V\) átoltottság esetén a védettek aránya nem \(V\) lesz, mint eddig, amíg tökéletes vakcinát feltételeztünk, hanem csak \(V\cdot VE_{\textrm{primer}}\) (hiszen az oltottak közül csak \(VE_{\textrm{primer}}\) arány válik ténylegesen is védetté). Tehát \(P=V\cdot VE_{\textrm{primer}}\), így az \(R_0\left(1-P\right)=R_0\left(1-V\cdot VE_{\textrm{primer}}\right)>1\) feltételt kell átrendeznünk \(V\)-re, amit elvégezve a következő kritériumot nyerjük a szükséges átoltottságra:
\[
V<\frac{1-\frac{1}{R_0}}{VE_{\textrm{primer}}}.
\]
Megkaptuk tehát, hogy nem tökéletes vakcinát használva mekkora átoltottságot kell elérnünk ahhoz, hogy a nyájimmunitást fenntartsuk, és ilyen módon megakadályozzuk járványok kitörését. Jól látható, hogy ez immár két dologtól függ: a betegség ragályosságától, és a rendelkezésre álló oltóanyag hatásosságától – minél nagyobb az előbbi, illetve minél kisebb ez utóbbi, annál nagyobb átoltottságra lesz szükség. Ezt az átoltottsági küszöböt néhány fontos védőoltással megelőzhető fertőző betegségre, és pár tipikus oltás-hatásosságra a következő táblázat mutatja, az eddigi táblázatok folytatásaként.
A legfontosabb védőoltással megelőzhető fertőző betegségek elemi reprodukciós számai (közelítő minimum és maximum a fejlett országokban) és az ezek alapján számolható, nyájimmunitáshoz szükséges minimális átoltottság, különböző primer vakcina-hatásosságok mellett, szekunder értelemben tökéletes vakcina esetén, a természetes immunitást elhanyagolva (a 100% feletti érték azt jelenti, hogy az adott esetben tökéletes nyájimmunitás nem érhető el oltással)
| Betegség | \(R_0\) | Primer vakcina-hatásosság | ||||
| 80% | 90% | 95% | 98% | 100% | ||
| Kanyaró | 12 | 114,6% | 101,9% | 96,5% | 93,5% | 91,7% |
| 18 | 118,1% | 104,9% | 99,4% | 96,4% | 94,4% | |
| Mumpsz | 4 | 93,8% | 83,3% | 78,9% | 76,5% | 75,0% |
| 7 | 107,1% | 95,2% | 90,2% | 87,5% | 85,7% | |
| Rubeola | 6 | 104,2% | 92,6% | 87,7% | 85,0% | 83,3% |
| 7 | 107,1% | 95,2% | 90,2% | 87,5% | 85,7% | |
| Diftéria | 6 | 104,2% | 92,6% | 87,7% | 85,0% | 83,3% |
| 7 | 107,1% | 95,2% | 90,2% | 87,5% | 85,7% | |
| Szamárköhögés | 12 | 114,6% | 101,9% | 96,5% | 93,5% | 91,7% |
| 17 | 117,6% | 104,6% | 99,1% | 96,0% | 94,1% | |
| Polio | 5 | 100,0% | 88,9% | 84,2% | 81,6% | 80,0% |
| 7 | 107,1% | 95,2% | 90,2% | 87,5% | 85,7% | |
| Tetanusz | 0 | - | - | - | - | - |
Érdemes felhívni a figyelmet, hogy itt már 100% feletti szükséges átoltottság is előfordul: ez értelemszerűen azt jelenti, hogy az adott betegségnél az adott hatásosságú oltással lehetetlen teljes körű nyájimmunitást elérni. Az egyéni védelem persze ettől még ugyanúgy fontos lehet, de tökéletes indirekt védelmet az oltatlanoknak nem tudunk biztosítani (tökéletlent azért persze igen – épp úgy, ahogy az előbbi ábra mutatja).
Ahogy azzal majd folytatni is fogom, ez a modell, illetve a belőle adódó fenti táblázat még mindig meglehetősen közelítő jellegű, de az alapvető mondanivalót immár helyesen, elfogadható pontossággal mutatja, és a tartalma, következményei jól kommunikálhatóak laikusoknak is.
Még egy megjegyzés mielőtt továbbhaladunk: az összes eddigi modellünk ún. statikus modell volt, tehát nem foglalkoztunk időtényezővel. Nem törődtünk azzal, hogy a járványok hogyan haladnak időben, hogy a fertőzések mikor következnek be stb. Könnyen elképzelhetőek olyan körülmények, melyben az influenzának és a HIV-nek egyaránt 3 az elemi reprodukciós száma. Csak míg az előbbi úgy jön ki, hogy a betegek időegység alatt sok embert tesznek ki a fertőzésnek, ám rövid időn keresztül, addig az utóbbi esetében időegység alatt kevesebbet, ám hosszabb időn keresztül. De ha az elemi reprodukciós számuk ugyanaz, akkor a modellünk szerint ugyanúgy viselkednek, például – védettség hiányában – mindkettő járványt fog okozni. Ami igaz is, csak egészen más jellegűt: az influenza nagyon gyorsan fel fog futni, addig a HIV-nél sokkal-sokkal elnyújtottabb módon gyűlnek a fertőzöttek. Erről azonban nem ad számot a fenti modell!
Az ilyen és ehhez hasonló kérdések megválaszolásához az időtényezőt is figyelembe vevő, ún. dinamikus modellekre van szükség. Azért hoztam fel épp most ennek a témáját, mert a védőoltások másik tökéletlenségének, a szekunder tökéletlenségnek a vizsgálatához szükségképp dinamikus modellt kell használni, hiszen ez a fajta hatásossági hiba ("hogyan gyengül idővel a védelem") definíciószerűen időben lezajlódó jelenség.
E modelleknél, illetve általában a fentieknél kifinomultabb modelleknél már nem megyek bele a részletekbe – nem azért, mert ne lennének fontosak, épp ellenkezőleg, népegészségügyi szempontokból az ilyen modellek használata a célravezetőbb, hiszen pontosabban írják le a valóságot – ám felépítésük, matematikájuk jóval bonyolultabb is. Az összkép megértése szempontjából emiatt kevésbé tanulságosak most, de az irodalom bőségesen tárgyalja ezeket az epidemiológiai modelleket. Én itt most csak néhány – érdekes és tanulságos – végeredmény közlésére szorítkozom.
Kezdjük először a szekunder tökéletlenséggel! Egy lehetséges modell ennek vizsgálatára az ún. SIRV-modell. Ebben a védőoltás adta immunitás elvesztése nem egy adott időpontban történik, hanem – a valóságnak megfelelően – véletlenszerű: lesz, aki akár nagyon hamar elveszti, lesz aki egy emberöltőn át sem. A modell ezt egy ráta segítségével határozza meg: például 2% veszíti el az immunitását évente. (Tehát 100 immunis emberből az első évben 2 veszíti el immunitását, így a második év elején már csak 98 immunis marad, a második év során ennek is a 2%-a, tehát 1,96 ember elveszíti az immunitását, így a harmadik év elejére már csak 96,04 immunis marad és így tovább. A tizedik év végére már csak 81,7 immunis marad, az ötvenedik év végére már csak 36,4, a századik év végére már csak 13,3. Belátható, hogy ez egyúttal azt is jelenti, hogy a vakcina adta immunitás átlagos hossza \(\frac{1}{0,02}=50\) év.)
Ebben a modellben a szekunder tökéletlenség ugyanolyan szorzóként jelenik meg, mint a primer, tehát a ténylegesen védettek aránya: \(V\cdot VE_{\textrm{primer}}\cdot VE_{\textrm{szekunder}}\). A modell szerint \(VE_{\textrm{szekunder}}=\frac{\mu}{\mu+\omega}\), ahol \(\mu\) a halálozás, \(\omega\) pedig a gyengülés előbb említett rájáta. Például, ha \(\mu=0,\!015\) (kb. 67 év a várható élettartam), ekkor egy 50 éves várható védelmet adó vakcina (\(\omega=0,\!02\)) esetén a szekunder hatásosság mindössze 43%, de még várhatóan 100 év alatt gyengülő oltás hatásossága is csak 60%! Mindezt a következő ábra kék görbéje mutatja. (A szekunder hatásosság úgy is felfogható, mint ekvivalens primer hatásosság, a fenti példa számait használva: a fenti példát folytatva egy várhatóan 50 év alatt gyengülő vakcina egyenértékű egy nem gyengülő, de csak a beoltottak 43%-át megvédő védőoltással!) A szekunder hatásosság jelentősége tehát egészen meglepően nagy; még primer értelemben tökéletes vakcina esetén is fényévekre vagyunk attól a legtöbb betegség esetén, ami a nyájimmunitás kialakításához szükséges lenne.
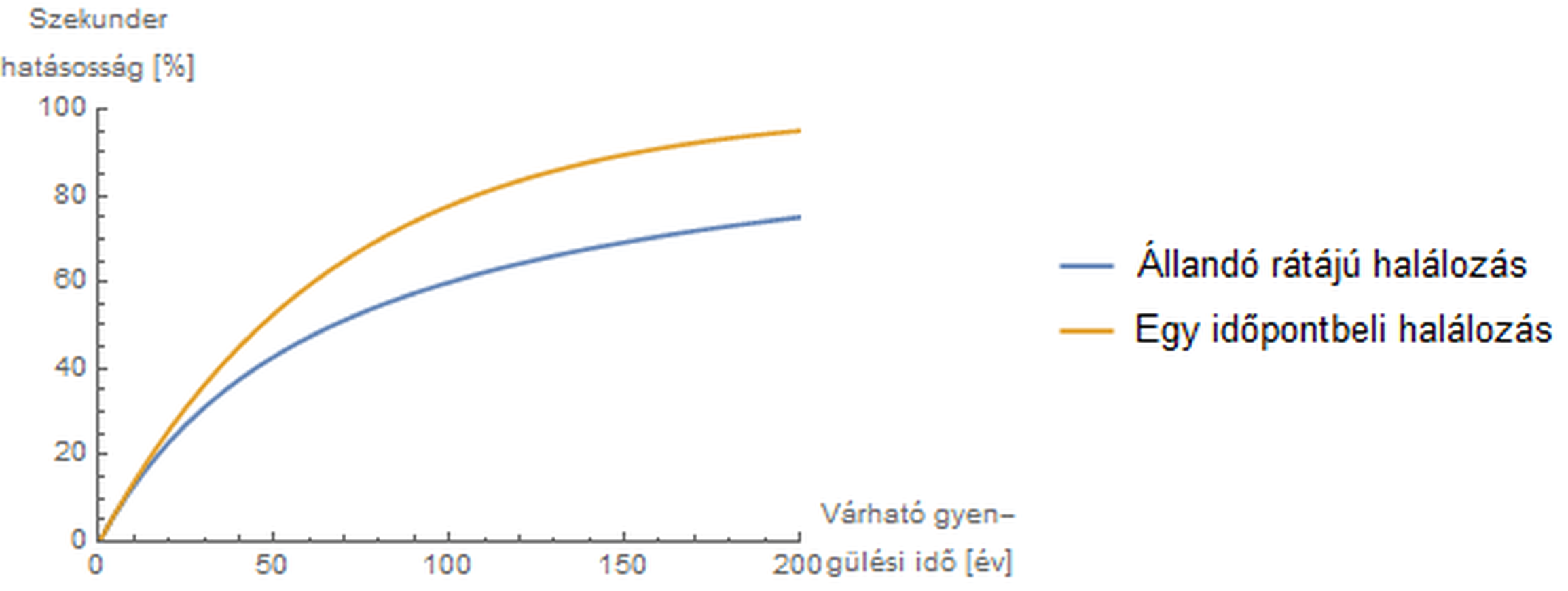
Védőoltás \(VE_{\textrm{szekunder}}\) szekunder hatásossága, az oltás gyengülésének várható ideje függvényében; kb. 67 év várható élettartam feltételezése, és kétféle korfa mellett: vagy 1,5%-os, állandó halálozási ráta (kék görbe), vagy mindenki megéri a várható élettartamot és akkor mindenki meghal (narancs görbe)
Mi erre a magyarázat? Hogyan lehet, hogy akkor mégis azt tapasztaljuk, hogy kialakítható nyájimmunitás védőoltásokkal, tehát, hogy szinte 100%-osan eltűntek betegségek, ráadásul nem is 100%-os átoltottság mellett és nem primer értelemben 100%-os hatásosságú vakcinák használatával? A vakcinák ennyire tökéletesek lennének szekunder szempontból, hogy a gyengülési rátájuk annyira kicsiny, ami több száz éves várható oltás adta védelemnek felel meg...? Nem, valószínűbb az a magyarázat, hogy itt már láthatóvá válik, hogy a modellünk a leegyszerűsítő feltevései miatt nem ragadja meg jól a valóságot. Amint utaltam is rá, a dinamikus modelleknél már elég sokféle feltételezéssel kell élnünk, és a SIRV-modell ezeknél szinte mindenhol a legegyszerűbbet választja.
Csak egyetlen példát kiragadva: meglehetősen irreális az a feltételezés, hogy a halálozási ráta állandó. Mert igaz ugyan, hogy \(\mu=0,\!015\) esetén 67 éves várható élettartamot kapunk (ami teljesen rendben van), csak épp, ha valaki utánaszámol, akkor kiderül, hogy ez a közelítés egyúttal olyanokat is jelent, hogy a lakosság mintegy 22%-a 100 évnél is tovább él! Várható élettartamban tehát stimmel a modell, de az egész korfát nagyon gyatrán ragadja meg. Ennél még az is jobb közelítés, ha azt mondjuk, hogy a várható élettartamot kivétel nélküli mindenki megéli, viszont pontosan akkor mindenki meghal. Persze, nyilván ez sem igaz, de – különösen a fejlett világban – ez a korfa még mindig közelebb van a valóságos korfákhoz mint az előbbi, állandó halálozási ráta feltételezése melletti. Márpedig ha áttérünk erre az "egy időpontbeli halálozás" közelítésre, akkor a szekunder hatásosság is rögtön megnyugtatóbb képet fest: az előbbi ábrán a narancs színű görbe mutatja az így kapott értékeket – jól látható, hogy ugyanazon oltás-gyengülés mellett is mennyivel nagyobb a szekunder hatásosság ezzel a reálisabb modellel, mint az előzővel. Ez tehát egy jó példa arra, hogy a valódi viszonyok pontosabb figyelembevétele a modellt is közelíti a valósághoz.
Ez persze csak egy – pusztán illusztrációt szolgáló – apróság volt, de megtehetjük, hogy ehhez hasonlóan kijavítjuk a modellt más pontokon is, illetve, hogy még további részleteket építünk be – hogy a nagyobb bonyolultság árán realisztikusabb eredményt kapjunk. Erre mutat példát a következő ábra, mely egy összehasonlíthatatlanul komplexebb modell eredményeit mutatja, ami ráadásul nem csak a népességszintű jelenségeket, hanem az egyéni immunológiai folyamatokat is modellezi.
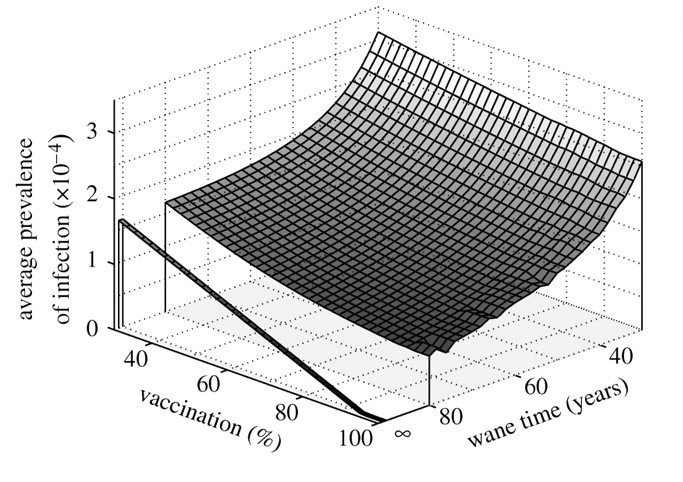
Az oltás szekunder tökéletlenségének – az oltás adta védelem időbeli gyengülésének – a hatása a betegség előfordulására (a bal oldali tengelyen az átoltottság, a jobb oldali tengelyen a védelem gyengüléséhez szükséges idő, a függőleges tengelyen a betegség előfordulása)
A végtelen gyengülési idő a szekunder értelemben tökéletes vakcinát jelenti, így ennek a görbéje megfelel annak, amit már mi is láttunk a korábbi ábrán. A mellette lévő felületen jól látható a szekunder tökéletlenség hatása. Kevésbé drámai, mint ami a SIRV-modellnél adódott, azonban így is jól látható, hogy a szekunder értelmű tökéletlenségnek igen komoly hatása lehet.
Mi a különbség oka, miben jobb ez a modell, mint a SIRV? A számos eltérés közül kiemelendő az a tény, hogy nem feltételezi, hogy az oltás hatása "mindent vagy semmit". A SIRV-modellben az ugyan véletlenszerű volt, hogy mennyi idő alatt gyengül a védelem, azonban a gyengülés maga bináris volt: az alany a tökéletesen védett állapotból a tökéletesen fogékonyba került át. Ez nyilván nem életszerű, hiszen a valóságban a védelem nem bináris, a kettő között vannak fokozatok. Ez nem csak modellezési, hanem orvosi kérdés is: ha valakinek gyengül az oltás adta védelme és emiatt mondjuk kanyarós lesz az oltás ellenére is, az várhatóan akkor sem ugyanolyan kanyaró lesz, mint egy betegséggel vagy oltással soha nem találkozott alany esetében, hanem egy enyhébb lefolyású – adott esetben akár klinikai tünetekkel nem, vagy alig járó – megbetegedés, hiszen attól még, mert az immunitása a megbetegedést nem tudta megakadályozni, nem nulla a jelentősége. (A kérdés azért is érdekes, mert egyes feltételezések szerint ez a mechanizmus is közrejátszik abban, hogy a kanyaró miért tud relatíve nagy átoltottságú populációkban is kitörni.)
Megjegyzem, ugyanez már a primer értelmű hatásosságnál is megtárgyalható lett volna. Gondoljuk csak végig, ott ugyanez a kérdés felvethető lett volna: amikor azt mondjuk, hogy "80%-os" a primer hatásosság, az alatt mit értünk? Azt, hogy a beoltottak 80%-a tökéletesen immunis lesz, a többi pedig semennyire, vagy azt, hogy mindenki 80%-os erősségű védettséget nyer...? Mi eddig az előbbit értettük ez alatt, de pusztán az egyszerűsítés kedvéért: az utóbbi is ugyanolyan értelmes lehetőség, csak épp ahhoz már figyelembe kell venni a nem-bináris immunitást, tehát, hogy ha valakit beoltottunk, és védetté is vált, az sem jelenti, hogy lehetetlen, hogy elkapja a betegséget – csak csökkenti a kockázatát. Ez azonban a lényegen nem változtat: mindkét esetben ugyanúgy 80%-kal csökken az effektív reprodukciós szám az elemihez képest. Az mindegy,
- hogy a beoltottak 81%-a tökéletesen védett lesz, a többi pedig semennyire,
- vagy, hogy minden beoltott 81%-os erejű védelmet nyer (értve a fenti értelemben, tehát, hogy ennyivel csökken a megbetegedési kockázata, ha exponáljuk a kórokozónak),
- vagy, hogy az alanyok 90%-a 90% erejű védelmet nyer, a többi pedig semennyit,
a lényeg, hogy mindhárom esetben 100 embert exponálva a kórokozónak (elemi reprodukció) 81 fog ténylegesen megbetegedni (effektív reprodukció). Mondhatjuk például, hogy a védetté válás arányát egy \(VE_{\textrm{primer,arány}}\) jelű tényezővel mérjük, a védelem erősségét pedig egy \(VE_{\textrm{primer,erősség}}\) jelűvel (mennyivel csökken a megbetegedési kockázatom, ha be vagyok oltva és védetté váltam), ekkor a korábban definiált primer hatásosság: \(VE_{\textrm{primer}}=VE_{\textrm{primer,arány}}\cdot VE_{\textrm{primer,erősség}}\); az \(\frac{1-\frac{1}{R_0}}{VE_{\textrm{primer}}}\) nyájimmunitás fenntartásához minimálisan szükséges átolttság pedig marad változatlan.
Mindent egybevetve azt mondhatjuk, hogy a vakcináknak háromféle tökéletlenségük lehet: mekkora aránya válik védetté a beoltottaknak (primer hatásosság egyik komponense, \(VE_{\textrm{primer,arány}}\)), a védettek milyen erősségű védelmet nyernek (primer hatásosság másik komponense, \(VE_{\textrm{primer,erősség}}\)) és végül az oltás adta védelem hogyan gyengül időben (szekunder hatásosság, \(VE_{\textrm{szekunder}}\)).
Visszatérve a dinamikus modellekre, egy másik, nagyon érdekes következmény, ami ilyen modellekből kiolvasható (azaz, ami az események időbeli lefutásán múlik), az az ún. vakcinációs "mézeshetek" ("honeymoon") effektus. Ezt a SIRV-modellen a következő ábra mutatja.
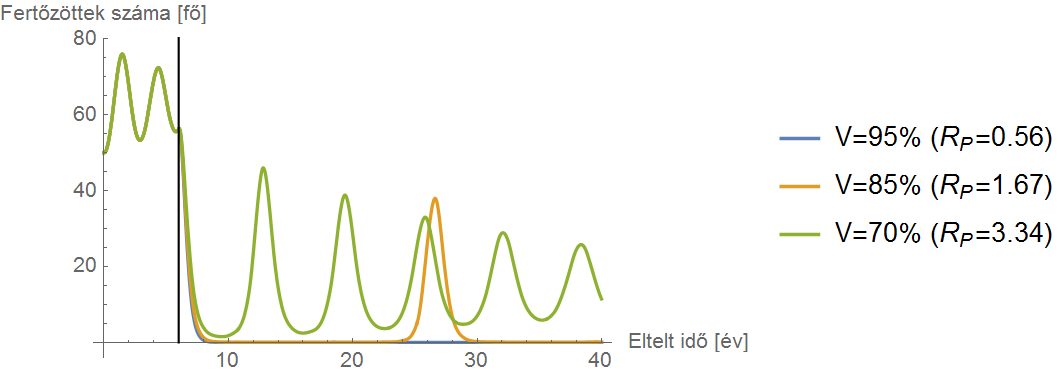
A vakcinációs "mézeshetek" ("honeymoon") effektus: egy 11 körüli elemi reprodukciós számú betegség ellen a 6. évben oltási programot indítunk, primer és szekunder értelemben egyaránt tökéletes vakcinával; az ábra a későbbi történéseket mutatja három különböző átoltottság, 95%, 85% és 70% mellett (a zárójelben lévő számok az így kialakuló effektív reprodukciós számot mutatják)
Az ábra egy olyan SIRV-modellt mutat, melynek a paramétereit úgy állították be, hogy nagyjából megfeleljen a fejlett országok kanyaró-helyzetének. (Figyeljük meg, hogy milyen szépen hozza a védőoltás bevezetése előtti érában, tehát az első 5 évben, a kanyaró valóságban is tapasztalt kétéves ciklusú ingadozását, melyről már itt is volt szó.) A 6. évben elindítunk egy oltási programot, primer és szekunder értelemben egyaránt tökéletes vakcinával. Az ábra három szcenárió esetén mutatja a későbbi történéseket (40 évre előre), melyek közül kettőben semmi meglepő nincs. Ha az átoltottság meghaladja a nyájimmunitás eléréséhez szükséges – itt 91% körüli – kritikus szintet (kék vonal), akkor az effektív reprodukciós szám 1 alá esik, a betegség az oltás bevezetése után gyorsan eltűnik, majd végleg meg is szűnik. Ha az átoltottság lényegesen elmarad a szükségestől (zöld vonal, 3 feletti effektív reprodukciós szám), akkor az oltás nem tudja felszámolni a betegséget: a periodikus járványok ugyanúgy megmaradnak, legfeljebb kicsit ritkábban jönnek és egy alkalommal kevesebb embert érintenek. Mindkét következmény teljesen logikus, eddig tehát semmi meglepőt nem találtunk. Az igazán érdekes a harmadik szcenárió: ha az átoltottság ugyan alacsonyabb, mint a szükséges – de csak kicsit (narancssárga vonal). Ebben az esetben ugyanis valami egészen meglepő történik: a betegség látszólag eltűnik, eleinte teljesen ugyanúgy, mint a sikeres felszámolás esetén, azonban egyszer csak, a szó legszorosabb értelmében a semmiből, minden előzmény nélkül, berobban egy járvány. Ami igazán megdöbbentő, hogy ez akár évtizednyi késleltetéssel is történhet! Mialatt megbetegedés nem fordul elő, minden szempontból úgy tűnhet, hogy a betegséget felszámoltuk, a kék és a narancssárga görbe gyakorlatilag egymáson fut. Ez a vakcinációs "mézeshetek" ("honeymoon") jelensége.
Mi a jelenség magyarázata? Az, hogy ha az effektív reprodukciós szám nagyobb ugyan 1-nél, de csak kicsivel, akkor igen lassan gyűlnek a fogékonyak, akik körében a járvány majd később berobbanhat. Ez alatt megbetegedés nem fordul elő, mert a fogékony halmaz nem elég nagy ahhoz, hogy önfenntartó terjedés tudjon benne beindulni. Amint azonban eléri a kritikus méretet, szinte az egész populáción végig tud futni a járvány. A meglepő az, hogy mindehhez éves, évtizedes idő is kellhet!
A bejegyzés itt folytatódik.