Úgy döntöttem, hogy – a nyomtatott könyvhöz hasonlóan – az alumíniummal foglalkozó írásomban szereplő részletszámításokat a blogon is más helyre rakom (hogy azt az írást ne feszítse nagyon szét a sok technikai részlet). Fenntartva persze, hogy amióta az itt leírtakra rájöttem, ezt az egész kinetikai számításos kérdéskört nem érzem túl fontosnak, lévén, hogy a védőoltás-elleneseknek e kérdésben már a kiindulópontja is helytelen.
Itt tehát azt fogom vizsgálni, hogy a védőoltásokból származó alumíniumterhelés hogyan viszonyul az anyatejből (illetve általában: a táplálkozásból), tehát a teljesen természetes forrásból származó alumíniumterheléshez. Másodlagosan bemutatom azt is, hogy mindez hogyan viszonyul az elfogadott beviteli limitekhez – szigorúan csak amolyan kiegészítésképpen. Legjobb tudomásom szerint ez lesz az első magyar viszonyokra vonatkozó számítás ebben a témában. (Ezt most kivételesen csak részben szánom kritikának a magyar szervek felé, hiszen a vakcinák biztonsága szempontjából nyilván nem oszt és nem szoroz, hogy valaki átszámítja-e a nemzetközi irodalmat pl. a magyar oltási naptárra – de más részről azt gondolom, hogy az anyukák megnyugtatása szempontjából viszont nagyon nem mindegy! Ennyiben tehát mégiscsak kritika, hogy idáig ezt senki nem tette meg; én legalábbis semmi ilyennek nyomát sem találtam a hivatalos magyar szervek oldalain.) A dolog teljesen nem elhanyagolható, hiszen például az amerikai oltási rend mind oltásaiban, mind azok ütemezésében eltér a magyartól. Természetesen szakmai értelemben nem sok újdonság lesz ebben az írásomban – végeredményben csak ,,testreszabom'' a nemzetközi irodalmat a magyar viszonyokra (magyar oltási naptár, magyar oltóanyagok, magyar gyermekek antropometriai adatai).
A számításokat Wolfram Mathematica 9.0 alatt végeztem; a felhasznált munkafüzetet – részint az általam mindig is hangsúlyozott transzparencia jegyében, részint konkrétan azért is, hogy a munkám ellenőrzését segítsem – teljes terjedelmében nyilvánosságra hozom, innen letölthető.
Alapmegoldás
Ebben a pontban tehát úgy vetem össze a természetes forrásokból és a védőoltásokból származó alumínium-bevitelt, hogy kiszámolom az ún. terhelést, ami a két forrásból származik. (Terhelésen azt értjük, hogy a szervezetben mennyi alumínium található adott időpillanatban az adott forrásból.) Ennek a kiszámításához természetesen bizonyos modellfeltevésekkel kell majd élni; itt az lesz a jellemző, hogy még kevés modellfeltevést használok, ezért csak közelítő (de cserében robusztus) megoldás nyerését várhatjuk. Később, a következő pontban, finomítani fogom az itteni modellt valósághűbb szempontok bevonásával.
Az első életévre fogok számolni, mert egyrészt ekkor kapja a gyermek az alumínium-tartalmú oltások többségét, másrészt későbbiekben mind a testtömege, mind a táplálkozási alumínium bevitele annyira megnő, hogy fel sem merül a toxicitás kérdése.
Ebben a pontban a nem jelölt modellfeltevések (valamint egyáltalán: a számítás logikája és menete) Keith és mtsai cikkéből valamint Mitkus és mtsai cikkéből származnak.
Táplálkozásból származó természetes alumíniumterhelés
Ahhoz, hogy meghatározzuk, hogy egy csecsemő szervezetében adott időpillanatban mennyi természetes forrásból származó alumínium van, szépen végig fogunk menni azon az útvonalon, ahogy az bejut a szervezetébe: mennyi alumínium van az anyatejben (tápszerben), ennek mekkora része kerül be a szisztémás keringésbe, ami bekerült, az mennyi ideig marad ott? – ebben a pontban ezekre a kérdésekre fogunk válaszokat keresni.
A táplálkozással bevitt alumínium mennyisége
A kutatást ott kell kezdenünk, hogy egyáltalán mekkora az a mennyiség, ami alumíniumból az anyatejjel (tápszerrel) bejut az emésztőrendszerbe.
Az anyatej alumínium-koncentrációja a mérések szerint két nagyságrendet átfogó biológiai variabilitást mutat, leírtak már 5 \(\mu\)g/l és 380 \(\mu\)g/l koncentrációt is. A tipikus érték 40 \(\mu\)g/l. A tápszerek átlagosan 225 \(\mu\)g/l, maximálisan 700 \(\mu\)g/l alumíniumot tartalmaznak. (Keith és mtsai eredeti cikkében 1150 \(\mu\)g/l szerepelt, én ezt azonban egy frissebb közlemény alapján kicsit mérsékeltem – ezzel is a védőoltások biztonsága ellen dolgozva) A bevitt táplálék (legyen az akár anyatej, akár tápszer) alumínium-koncentrációjára a továbbiakban egységesen a \(c\) jelölést fogom alkalmazni.
Ehhez még egy dolgot kell hozzávennünk: egy csecsemő a születésekor napi \(V_{\text{min}}=670\) ml folyadékot fogyaszt el, féléves korára ez napi \(V_{\text{max}}=900\) ml-re nő. Az egyszerűség kedvéért tételezzük fel, hogy a kettő között lineáris az átmenet. Ezen információk birtokában már meghatározható a bevitt alumínium mennyisége az első fél évben; a második fél évre – a félszilárd táplálkozásra történő áttéréssel – azt feltételezem az irodalmi adatok alapján, hogy az alumínium bevitt mennyisége napi \(m_{\text{ss}}=0,\!7\) mg.
Mindezeket egybevetve a táplálkozással bevitt alumínium napi mennyisége:
\[
\widetilde{m}_{c,V_{\text{max}},V_{\text{min}},m_{\text{ss}}}\left(t\right)=\begin{cases} \left[V_{\text{min}} + \frac{t}{6 \cdot 30} \cdot \left(V_{\text{max}}-V_{\text{min}}\right)\right] \cdot c \quad \text{ha } t<6 \cdot 30\\m_{\text{ss}} \quad \text{ha } t \geq 6 \cdot 30\end{cases},
\]
ahol \(t\) az idő, napban mérve.
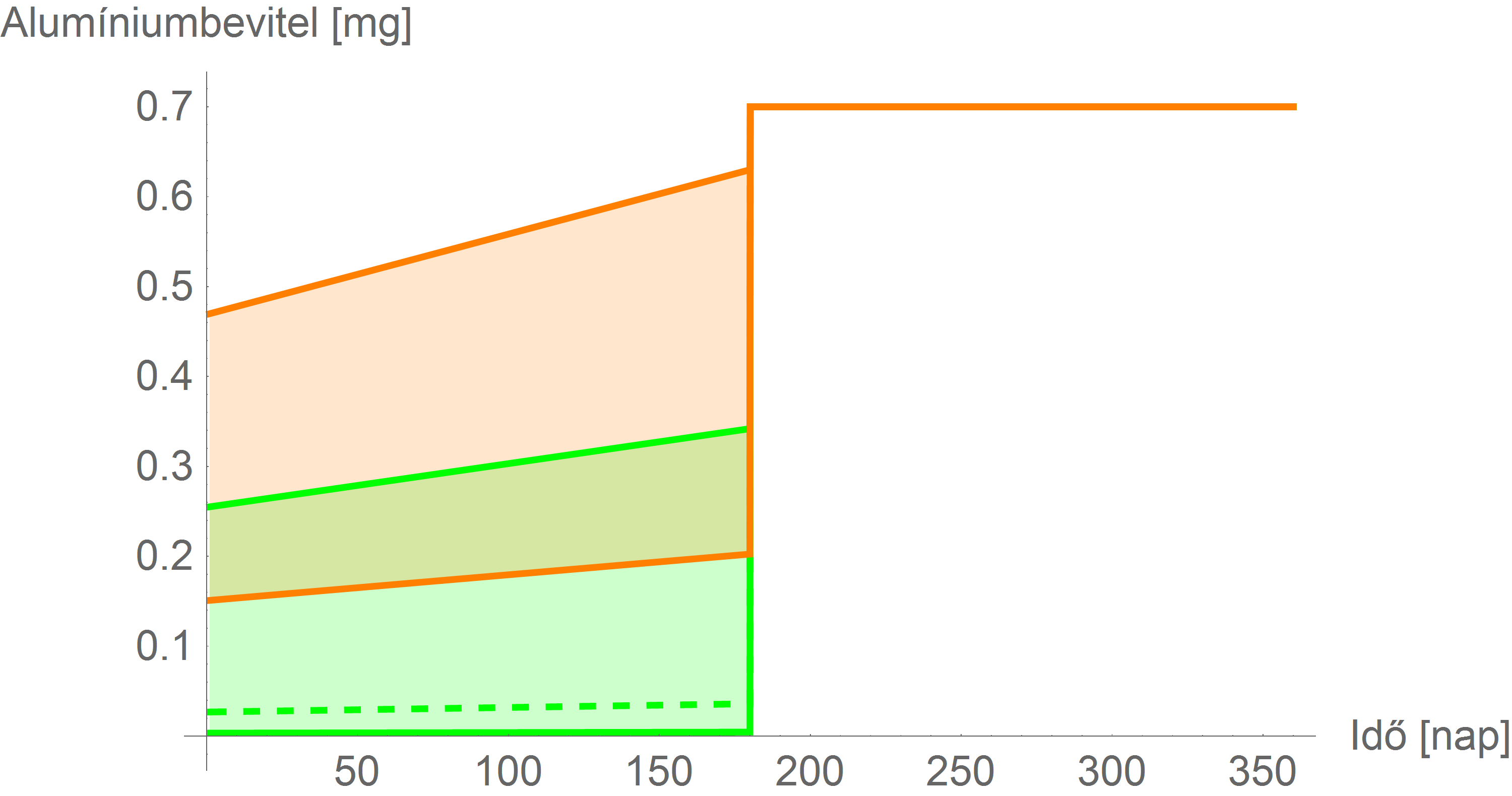
Ezt a függvényt a következő ábra szemlélteti (zöld az anyatejjel, narancssárga a tápszerrel bevihető mennyiség tartománya; az anyatej esetében szaggatott vonal a tipikus értéket jelöli):
Az alumínium biohasznosulása
Ezzel azonban még nem vagyunk kész, hiszen a megevett alumínium természetesen nem kerül be mind a szisztémás keringésbe – azaz, figyelembe kell venni a felszívódást. Szép szóval: ez az orális biohasznosulás kérdése. Már említettem is, hogy alumíniumnál ez rendkívül fontos kérdés, hiszen – szemben a formaldehiddel – a felszívódási faktor nagyon kicsi (százalék alatti) – épp emiatt nem lehet a kérdést, szemben a formaldehiddel, „ránézésre“ eldönteni. Ezt az orális biohasznosulást \(F_{\text{táplálék}}\)-kal jelölve (utalva arra, hogy ez a táplálékkal bevitt alumínium biohasznosulása), a következő képletet kapjuk a szisztémás keringésbe kerülő (tehát már nem egyszerűen a bevitt) alumínium napi mennyiségére:
m_{c,V_{\text{max}},V_{\text{min}},m_{\text{ss}},F_{\text{táplálék}}}\left(t\right)=\begin{cases} \left[V_{\text{min}} + \frac{t}{6 \cdot 30} \cdot \left(V_{\text{max}}-V_{\text{min}}\right)\right] \cdot c \cdot F_{\text{táplálék}} \quad \text{ha } t<6 \cdot 30\\m_{\text{ss}} \cdot F_{\text{táplálék}} \quad \text{ha } t \geq 6 \cdot 30\end{cases}.
\]
A felszívódási faktort nem lehet egyértelműen megadni, mert a különböző vegyületek különbözőképp viselkednek: az orális biohasznosulás a 0,01 %-tól (alumínium-hidroxid) az 1 %-ig változik az irodalmi adatok alapján; ezen belül az alumínium-laktátra \(F_{\text{táplálék}}=0,\!78\) %-ot szoktak mondani, így a továbbiakban ezzel fogok számolni.
Az alumínium raktározódása
Raktározódáson (vagy retención) azt értjük, hogy abból az alumíniumból, ami egyszer bekerült a szisztémás keringésbe – tehát figyelem, nem csak bevittük, hanem már fel is szívódott! –, adott idő elteltével mennyi található meg még a szervezetben. (Hiszen attól még, mert bekerült, ki is kerül idővel, különféle kiürülési folyamatokon keresztül.)
Természetesen az erre vonatkozó kinetikai méréseket ténylegesen el is végezték. A klasszikus eredmény Priest és mtsaié, akik azt találták, hogy az alumínium szervezetbeni visszamaradását jól leírja a
\[
R\left(t\right) = 0,\!293 e^{-0,595t} + 0,\!114 e^{-0,172t} + 0,\!065 e^{-0,000401t}.
\]
függvény, ahol \(t \geq 1\) az eltelt idő, napban mérve. Ez egy ún. retenciós függvény, ami megadja, hogy a felvett (tehát mégegyszer: a szisztémás keringésbe bejutott, azaz nem egyszerűen a bevitt) alumínium mekkora része található meg a szervezetben adott \(t\) idő után. Úgy is fogalmazhatunk, hogy ha valaki szisztémás keringésébe bekerül 1 mg alumínium, akkor a fenti függvény mutatja, hogy abból a \(t\)-edik napon mennyi van még a szervezetében.
Az érzékeltetés kedvéért, ez a függvény így néz ki:
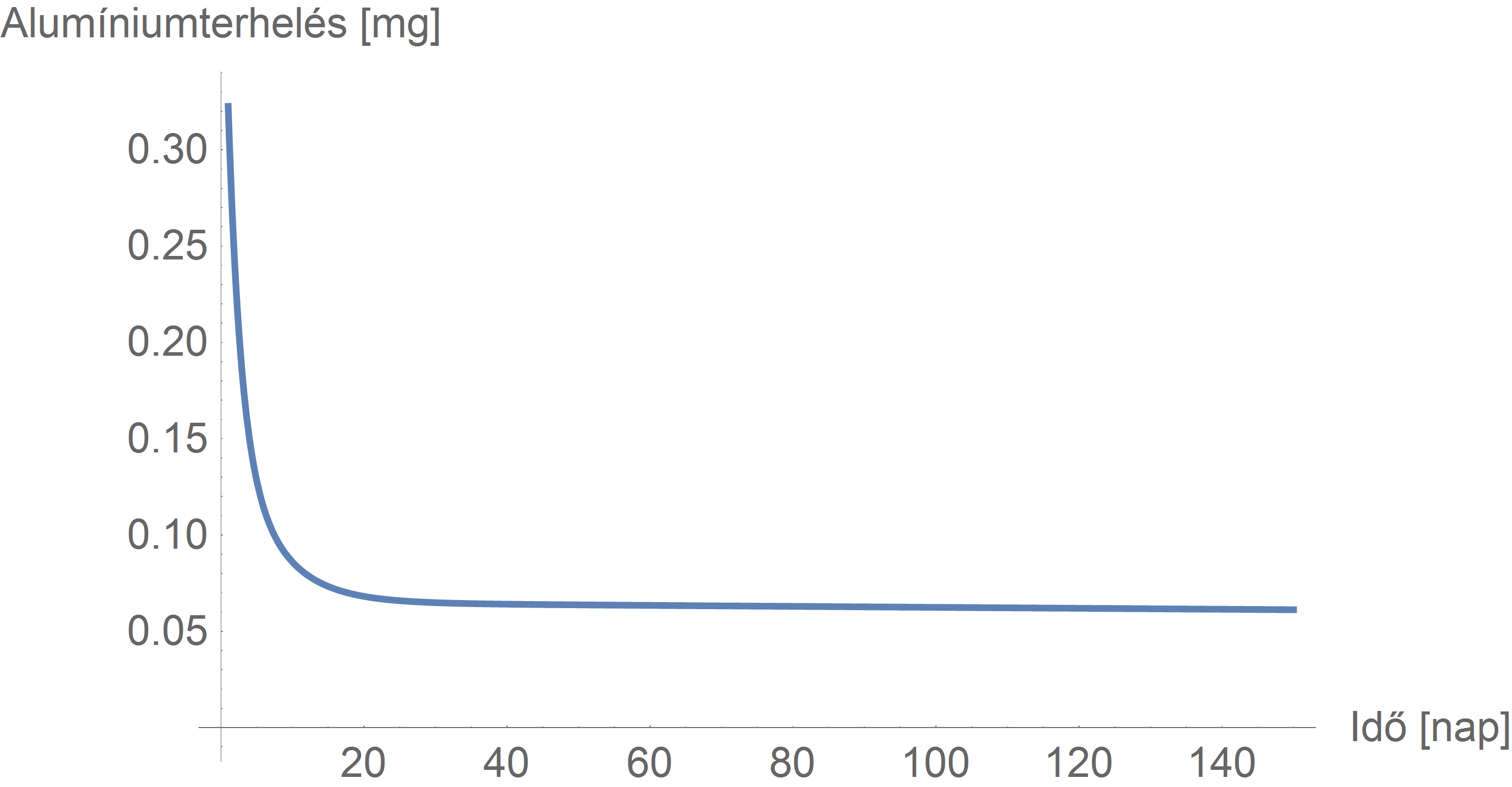
Látható, hogy a görbe három szakaszból áll: egy kezdeti nagyon gyors kiürülési szakaszból, egy középső, egész picit lassabb szakaszból (ez a kettő a fenti ábrán eléggé egybemosódik), és végül egy harmadik, drámaian lassabb végső kiürülési szakaszból. (Ezeket a fenti összegben szereplő egyes tagok képviselik. Láthatóan mindegyik exponenciális lecsengésű, így a biológiai felezési idő könnyen meghatározható: az első szakaszra \(\ln 2 / 0,\!595 = 1,\!2\) nap, a másodikra 4 nap, a harmadikra 1729 nap.)
Hangsúlyozom azt a fent már említett tényt, hogy a függvény csak a \(t \geq 1\) tartományra (tehát az első nap utáni viselkedésre) ad választ – szándékosan így becsülték meg, hogy elkerüljék a nagyon gyors változású, és emiatt bizonytalanabbul illeszthető első napot. (Ez magyarázza azt is, hogy \(0\)-ban miért nem \(1\) értéket vesz fel.) Ennek folytonos bevitel esetén (tehát a táplálkozásnál) értelemszerűen nincs jelentősége, de a védőoltások esetében majd lesz: ott e függvény használata az első napi terhelést nyilván alá fogja becsülni. A dolog azonban nem okoz problémát, hiszen azt még a védőoltás-ellenesek sem állítják, hogy az alumíniumnak akut toxicitása volna, így az első nap, jobban mondva inkább az első néhány óra – vegyük figyelembe ugyanis, hogy mérések szerint a vér alumínium-koncentrációja már a beadást követő 15 percben felére esik! – alábecslése nem sok vizet zavar; mi most úgyis a hosszútávú hatásokra leszünk kíváncsiak. A dolog már csak azért is fair, mert majd a táplálkozásnál sem fogunk a bevitel azonnali hatásával számolni. (Ráadásul amikor majd figyelembe vesszük a védőoltásokban lévő alumínium felszívódásának a kinetikáját, azaz, hogy ez a felszívódás nem azonnali, akkor az egész kérdés szinte okafogyottá válik.)
A fenti tri-exponenciális függvény egy háromkompartmentes kinetikának felel meg, egy centrális és két periferiális kompartmenttel, úgy, hogy kiürülés csak a centrális kompartmentből lehetséges. Ez a farmakokinetika egyik klasszikus modellje, így részletezés helyett inkább csak a modellt mutatom meg grafikusan:

Ez az ábra – érdekességként – tartalmazza azt is, hogy a feltételezések szerint mik az egyes kompartmentek anatómiai realitásai.
Az ábrán feltüntetett sebességi állandók a fenti retenciós függvényből meghatározhatóak, ez egy klasszikus farmakokinetikai feladat jól ismert megoldással, úgyhogy itt most csak a végeredményt közlöm:
\begin{align*}
k_{21} &= 0,\!2147 \text{ nap}^{-1} \\
k_{12} &= 0,\!0758 \text{ nap}^{-1} \\
k_{31} &= 0,\!000464 \text{ nap}^{-1} \\
k_{13} &= 0,\!065 \text{ nap}^{-1} \\
k_{10} &= 0,\!41095 \text{ nap}^{-1} \\
\end{align*}
Jelölje \(X_1\left(t\right)\), \(X_2\left(t\right)\) és \(X_3\left(t\right)\) az első, második és harmadik kompartmentben lévő alumínium mennyiségét rendre. Ezzel a jelöléssel a kompartmentális rendszer dinamikáját a következő három (lineáris, állandó együtthatós) differenciálegyenlet írja le:
\begin{align*}
\frac{\mathrm{d} X_1\left(t\right)}{\mathrm{d}t}&=-k_{10}X_1\left(t\right)+k_{21}X_2\left(t\right)+k_{31}X_3\left(t\right)-k_{12}X_1\left(t\right)-k_{13}X_1\left(t\right)\\
\frac{\mathrm{d} X_2\left(t\right)}{\mathrm{d}t}&=k_{12}X_1\left(t\right)-k_{21}X_2\left(t\right)\\
\frac{\mathrm{d}X_3\left(t\right)}{\mathrm{d}t}&=k_{13}X_1\left(t\right)-k_{31}X_3\left(t\right)\\
\end{align*}
az
\begin{align*}
X_1\left(t\right)&=0,\!293+0,\!114+0,\!065=0,\!472\\
X_2\left(t\right)&=0\\
X_3\left(t\right)&=0\\
\end{align*}
kezdeti feltételekkel.
Bárki ellenőrizheti, ha megoldja ezt a differenciálegyenlet-rendszert, hogy az valóban a fenti retenciós függvényt adja. Ezen a ponton felmerülhet a kérdés, hogy ha ezzel a kompartmentális hókusz-pókusszal végeredményban ugyanoda jutottunk el, akkor mi értelme volt az egésznek? A kérdés jogos, ezen a ponton még valóban semmi, de az elemzésünk későbbi továbbfejlesztéséhez szükségünk lesz a kompartmentális megközelítésre is.
Végeredmény
A fentiek tehát megadják, hogy egy egyszeri, szisztémás keringésbe került dózis (bólus) hogyan viselkedik: ha \(m\) dózis jut a szisztémás keringésbe, abból a \(t\)-edik napon \(m\cdot R\left(t\right)\) lesz még a szervezetben. Ez tehát például a vakcinák számításához kitűnően alkalmazható lesz; viszont a táplálkozás bonyolultabb ügy, hiszen az nem egyszeri, hanem ismétlődő bevitelt jelent. Különösen ebben a korban (napi sokszori táplálkozás) nem vétünk nagy hibát, ha elhanyagoljuk ennek a diszkrétségét, azaz úgy vesszük, hogy folytonos a bevitel. Ekkor persze az \(m\) jelentése már nem dózis, hanem ráta (dózis/nap); és az ebből származó terhelést – a folytonosságnak hála – egyszerű integrálással kapjuk:
\[
B_{c,V_{\text{max}},V_{\text{min}},m_{\text{ss}},F_{\text{táplálék}}}^{\left(\text{táplálék}\right)}\left(t\right)=\int_{s=0}^t m_{c,V_{\text{max}},V_{\text{min}},m_{\text{ss}},F_{\text{táplálék}}}\left(s\right) R\left(t-s\right) \mathrm{d} s.
\]
(Ne felejtsük el, hogy az integrandusban \(R\left(t-s\right)\)-sel kell rászoroznunk a beviteli rátára, nem \(R\left(s\right)\)-sel – a kettő csak időben állandó ráta esetén lenne mindegy!) Ez a konvolúciós integrál úgy is felfogható, mintha elcsúsztatott koncentráció-görbéket adtunk volna össze.
Behelyettesítve az eddig kiszámoltakat, és elvégezve az integrálást, meghatározható a táplálkozásból származó, szervezetben maradó összmennyiség, ezt nevezzük a továbbiakban alumíniumterhelésnek. Ezt a következő ábra mutatja (a színek jelentése ez eddigivel egyezik):
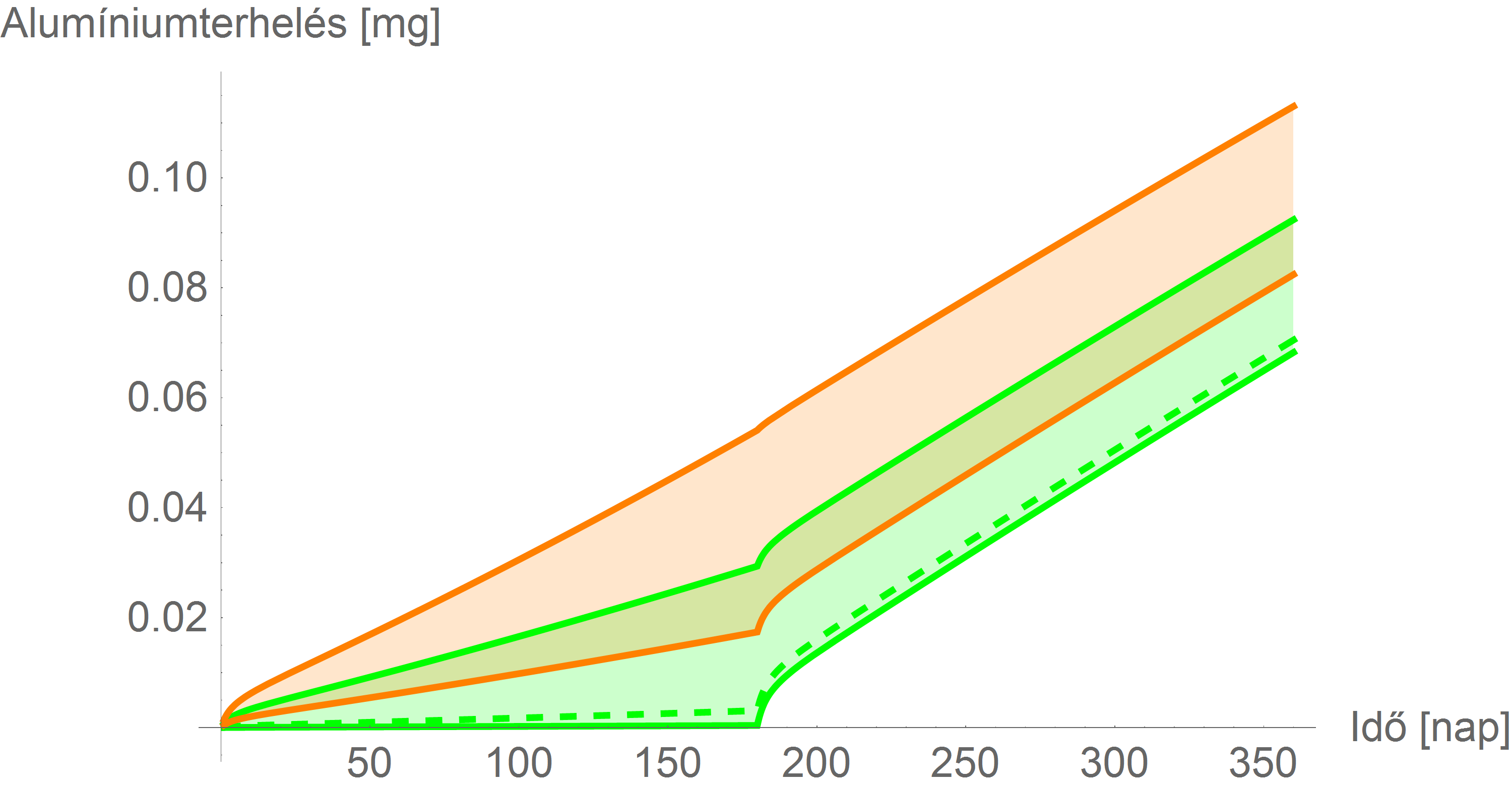
Védőoltásokból származó alumíniumterhelés
Az előzőek fényében a védőoltásokból származó alumíniumterhelés meghatározása igen könnyű lesz. A jelenleg hatályos, 2016-os Védőoltási Módszertani Levélen alapuló magyar oltási naptár szerint a számunkra releváns időszakban egy oltás van, ami nem tartalmaz alumíniumot (BCG), és kétszer három, ami igen (DTaP-IPV-Hib és PCV). Ez utóbbiakhoz jelenleg a Pentaxim és a Prevenar13 nevű oltóanyagot használják, az előbbi adagonként 0,3, az utóbbi 0,125 mg alumínium-hidroxidot tartalmaz; az előbbit a csecsemők 2, 3 és 4 hónapos korukban kapják, az utóbbit 2, 4 és 12 hónapos korukban. (Ezt a legutóbbit a csecsemőkori terhelés elemzésekor értelemszerűen nem veszem figyelembe, de a későbbi hosszabb távú elemzésekben természetesen igen.) Egyelőre feltételezem, hogy a védőoltásokban lévő alumínium biohasznosulása \(F_{\text{vakcina}}=100\) %, és, hogy felszívódásuk azonnali a beadás pillanatában. (Próbálok magam ellen csalni.)
Nincs más dolgunk tehát, mint (háromszor) alkalmazni a retenciós függvényt, és így megkapjuk a vakcinákból származó alumíniumterhelést:
\begin{split}
B^{\left(\text{vakcina}\right)}\left(t\right) &= \begin{cases} 0 \quad \text{ha } t < 60 \\ 0,\!425 \cdot R\left(t-60\right) \quad \text{ha } 60 \leq t < 90\\0,\!425 \cdot R\left(t-60\right) + 0,\!3 \cdot R\left(t-90\right) \quad \text{ha } 90 \leq t < 120\\ 0,\!425 \cdot R\left(t-60\right) + 0,\!3 \cdot R\left(t-90\right) + 0,\!425 \cdot R\left(t-120\right) \quad \text{ha } t \geq 120\end{cases}
\end{split}
\end{equation*}
Ezt a szokott módon grafikusan ábrázolva:
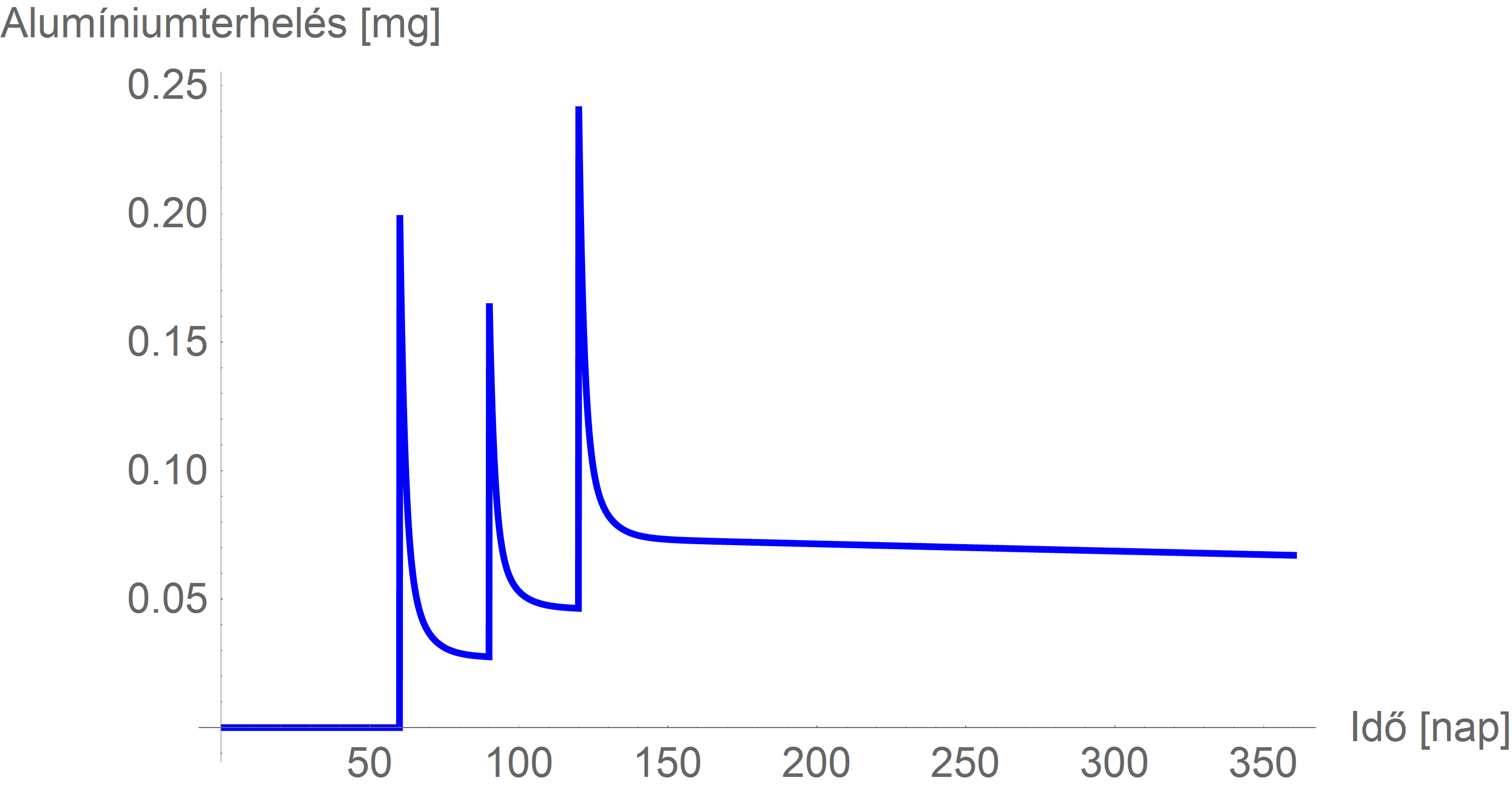
Beviteli limitek
A teljesség kedvéért, de hangsúlyozottan csak kiegészítés gyanánt, bemutatom azt is, hogy ez a terhelés hogyan viszonyul a nemzetközi határértékekhez. Tekintetbe véve, hogy e limitek bevitelre – és nem terhelésre – szabnak korlátot, így a fentiekkel való összevetéshez nyilván átszámítás szükséges: az engedélyezett terhelést úgy kapjuk meg, hogy feltételezzük, hogy az alany minden nap épp az engedélyezett bevitelt fogyasztja el. (Tehát kiszámítjuk, hogy mennyi alumínium lesz a szervezetében, ha a maximális engedélyezett bevitelt használja ki.)
Két alapvető szabványt érdemes megemlíteni a témában. Az egyik az amerikai ATSDR, mely az alumíniumra 1 mg/ttkg/nap ún. MRL-t (minimális kockázati szintet) állapított meg. (Az MRL az a szint, aminek bevitele valószínűsíthetően semmilyen kockázattal nem jár, adott végpont – alumínium esetében ez a védőoltás-ellenesek kedvence, a neurotoxicitás volt – tekintetében. Ráadásul konkrétan az alumínium limitje középtávú (14-364 nap) és krónikus (\(\geq\)365 nap) expozícióra vonatkozik, nem is epizodikusra, így még szigorúbb is, mint ami a védőoltások esetében releváns lenne.) A másik szabvány az európai EFSA 1 mg/ttkg/hét korlátja – az ATSDR-nél drasztikusan szigorúbb limit oka, hogy ezt arra tervezték, hogy akár egy egész életen át történő folyamatos ilyen mértékű bevitel is biztonságos legyen. A szabvány annyira ultra-biztonságos, hogy vizsgálatok szerint az európai népesség nagyobb része e pillanatban is átlépi, mégpedig védőoltásoktól teljesen függetlenül, a táplálkozásával (van, aki többszörösen…); ennek ellenére ezt is fel fogom használni viszonyításként, noha nyilván összehasonlíthatatlanul szigorúbb, mint ami valóban releváns lenne egy életünkben összesen néhányszor megismétlődő bevitelre.
További probléma, hogy a limitek testtömegre vannak megadva, így a belőlük adódó terhelés attól is függ, hogy milyen súlyú csecsemőről beszélünk. Azért, hogy a lehető legjobban csaljak a vakcinák ellen, referencia-csecsemőként egy 3. testtömegpercentilisen lévő lányt használtam – ez volt az irodalmi adatokban elérhető legkisebb testtömeg adott életkorra. (A 3. testtömegpercentilis jelenti azt a testtömeget, amiről elmondható, hogy az adott életkorú és adott nemű csecsemők 97 %-a ennél nagyobb tömegű.) Az adatokat a magyar Országos Longitudinális Gyermeknövekedés-vizsgálat eredményeiből vettem át. (Ez eleinte havonta, majd féléves kortól egyéves korig kéthavonta tartalmazza nemenkénti bontásban a 3, 10, 25, 50, 75, 90, 97 percentilis testtömegeket.) Adott napra vonatkozó testtömeget ezen adatokból harmadrendű interpolációval számoltam.
Ezek alapján a következő limiteket kapjuk alumíniumterhelésre (a magasabban futó görbe értelemszerűen az ATSDR-, az alacsonyabb az EFSA-szabvány alapján készült):
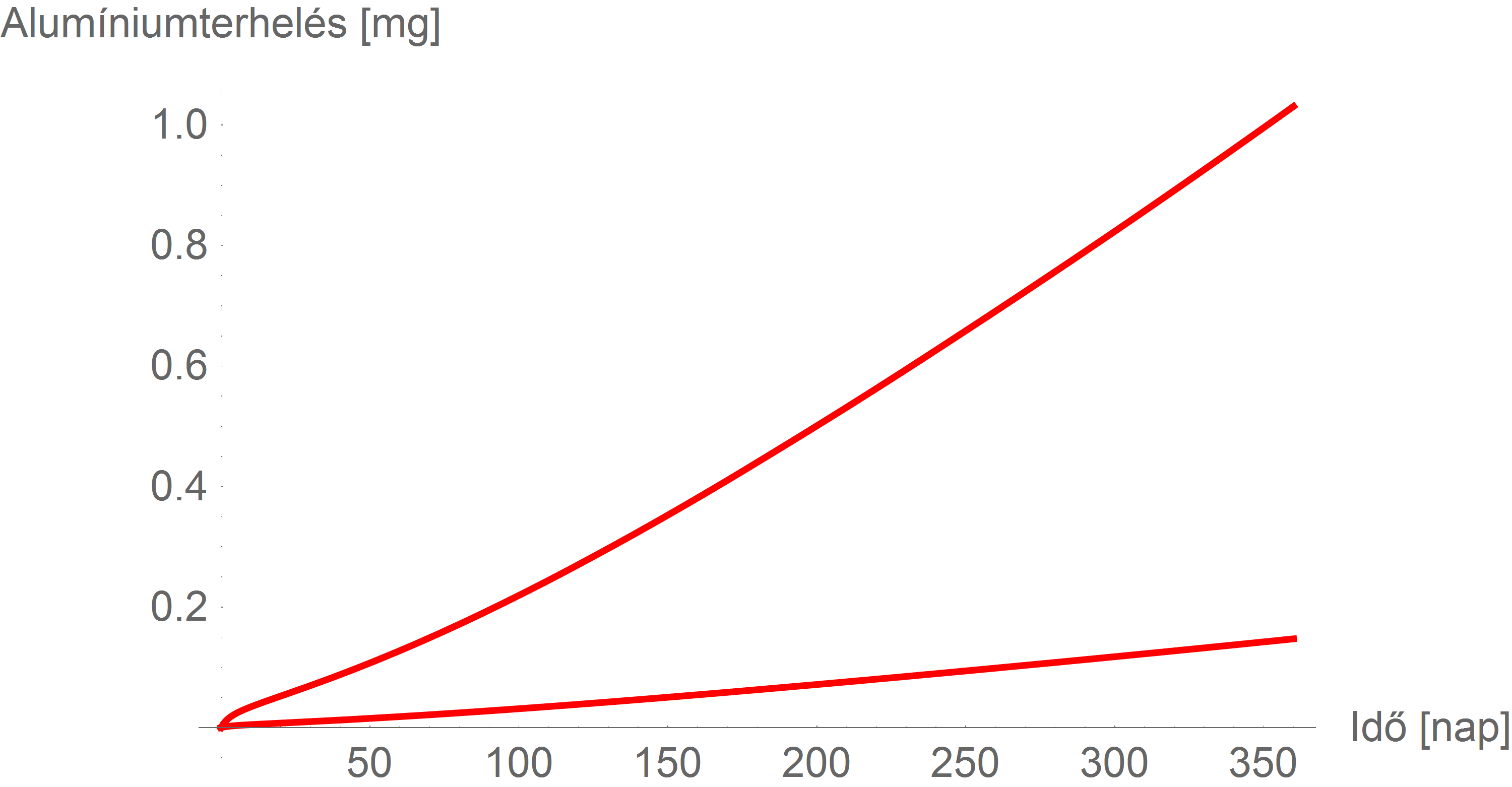
Mindent egybevetve
Ha most az összes eddigi eredményt egy ábrán jelenítjük meg, akkor a következő, a védőoltás biztonságosságának megítélése szempontjából kulcsfontosságú grafikonhoz jutunk:
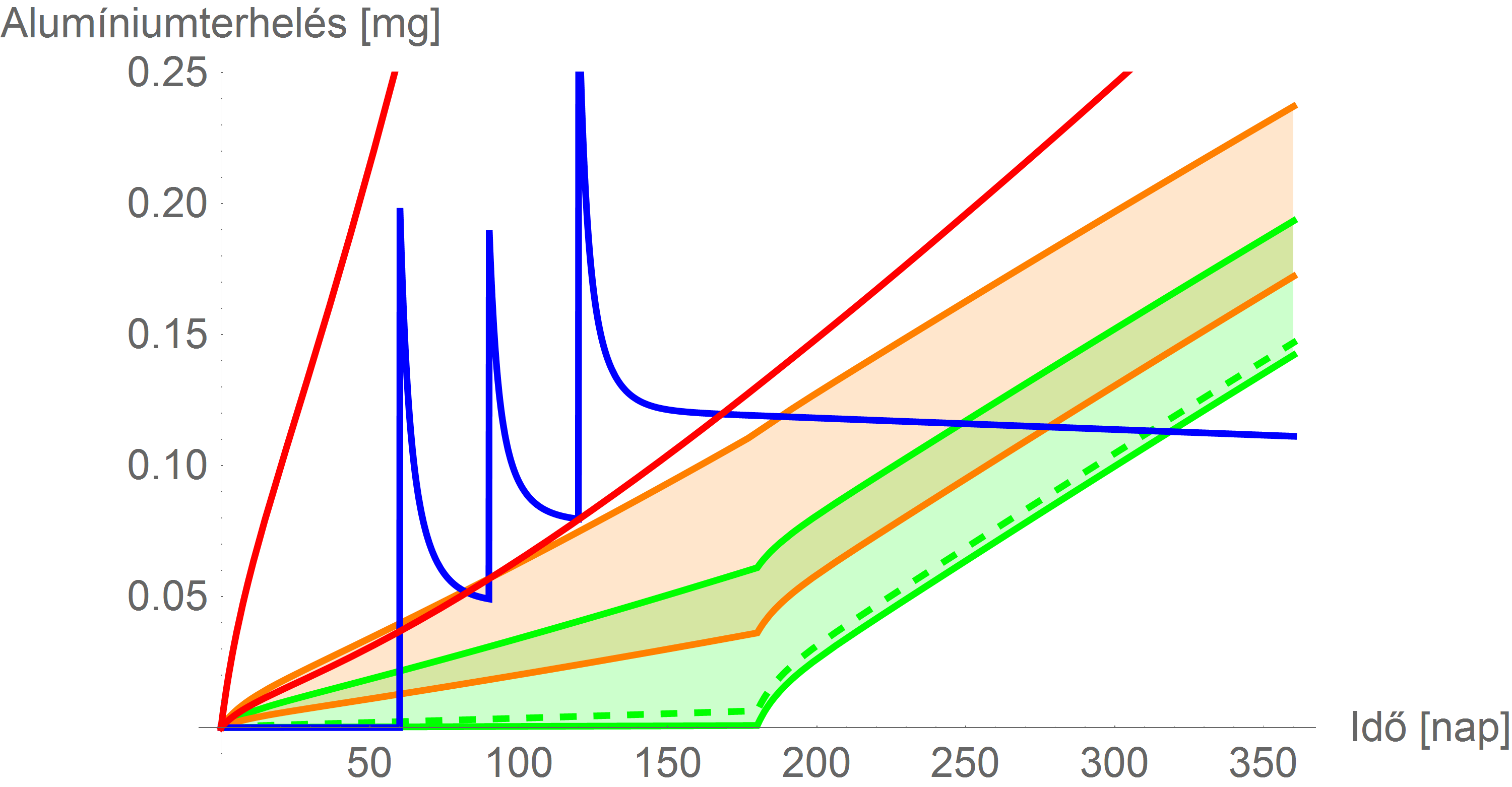
Jól látható, hogy az ATSDR-korlát rá sem fér az ábrára, ahhoz, hogy ezt ábrázolni tudjuk, még a függőleges tengelyt is át kell skálázni:
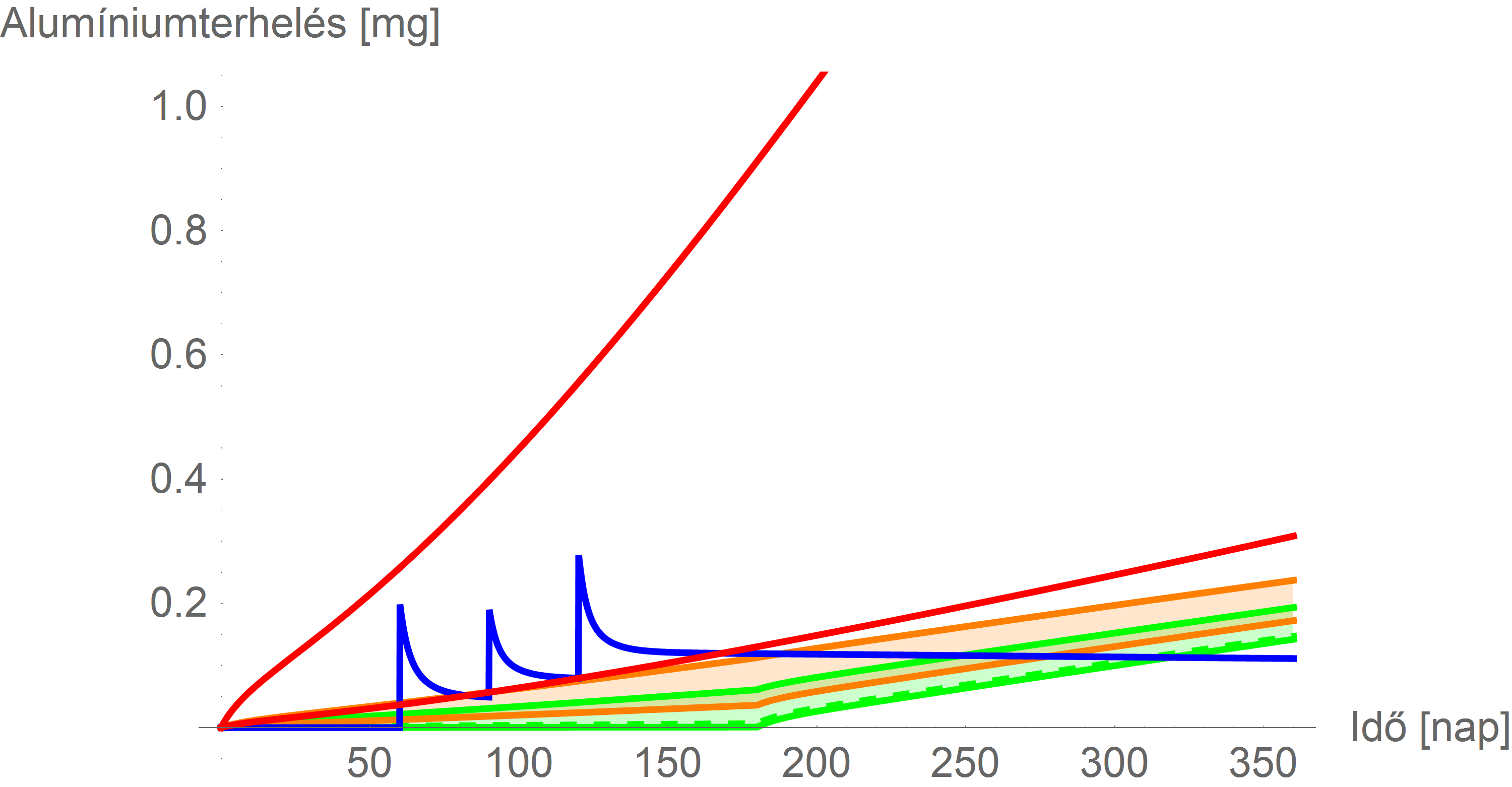
Az alapmegoldás finomítása
Ebben a pontban a fenti eredményeket fogjuk pontosítani azáltal, hogy finomabb észrevételeket is beépítünk a számításokba. Általánosságban is elmondható, hogy ezek a számítások – lévén, hogy újabb modellfeltevéseket tesznek szükségessé – rontják az eredmény robusztusságát, viszont a némileg nagyobb bizonytalanságért cserében lényegesen reálisabb, pontosabb képet adnak.
Ebben a pontban a nem jelölt modellfeltevések – valamint egyáltalán: a számítás logikája és menete – Mitkus és mtsai cikkéből származnak.
A glomeruláris filtráció fejlődésének figyelembevétele
Az egyik pont, ahol a fenti számításban csaltunk az, hogy a kompartmentek közötti időállandókat, így a kiürülés sebességállandóját is, egy felnőttön kimért adatsor alapján adtuk meg. Ez azért gond, mert csecsemőkben (különösen újszülöttekben) a glomeruláris filtráció, ami esetükben az alumínium eltávolításának legfontosabb útja, még fejletlen, így minden okunk megvan feltételezni, hogy náluk ez az állandó kisebb. (A dolog ugye azért nem mindegy, mert így mind a természetes – táplálkozásból adódó –, mind a vakcinákból származó felhalmozódó alumíniumterhelés rögtön nagyobb kell legyen, hiszen lényegében arról van szó, hogy az eltávolítás kevésbé hatásos.)
Ennek becsléséhez Mitkus és mtsai egy olyan vizsgálat eredményeit használták fel, mely több mint száz gyermek kreatinin clearance adatait mérte le 13 éven keresztül. (A kretinin clearance-ét a vesefunkció, így a glomeruláris filtráció hatásosságának hozzávetőleges jellemzésére használhatjuk.) Mivel ez a görbe kezdetben meredeken nő, aztán az életkor előrehaladtával kilaposodik, hogy aszimptotikusan elérje a felnőttkori értéket, a szerzők Michaelis–Menten-függvénnyel közelítették. Ennek alakja – átnormálva úgy, hogy az aszimptotikus érték 1 legyen –:
\[
f\left(t\right)=0,\!361+0,\!639\cdot\left(\frac{t}{t+231,\!462}\right).
\]
Ezt most alkalmazva az alumínium kiürülési állandójára, arra jutunk, hogy az ne egy \(k_{10}=0,\!41095\) nap\(^{-1}\) (időfüggetlen) konstans legyen, hanem egy időfüggvény:
\[
k_{10}\left(t\right)=f\left(t\right) \cdot 0,\!41095.
\]
Ezzel a kinetikát leíró differenciálegyenlet-rendszer:
\begin{align*}
\frac{\mathrm{d} X_1\left(t\right)}{\mathrm{d}t}&=-k_{10}\left(t\right)X_1\left(t\right)+k_{21}X_2\left(t\right)+k_{31}X_3\left(t\right)-k_{12}X_1\left(t\right)-k_{13}X_1\left(t\right)\\
\frac{\mathrm{d} X_2\left(t\right)}{\mathrm{d}t}&=k_{12}X_1\left(t\right)-k_{21}X_2\left(t\right)\\
\frac{\mathrm{d}X_3\left(t\right)}{\mathrm{d}t}&=k_{13}X_1\left(t\right)-k_{31}X_3\left(t\right)\\
\end{align*}
változatlan kezdeti feltételekkel.
A módosulás formailag minimális, de tartalmilag nagy, hiszen ez már nem állandó együtthatós rendszer, így nincs szimbolikusan előállítható megoldása. (Csak akkor lenne, ha az \(\mathbf{A}\left(t\right)\) együtthatómátrixra teljesülne az \(\mathbf{A}\left(t\right)\cdot\int_0^t \mathbf{A}\left(s\right) \mathrm{d} s = \int_0^t \mathbf{A}\left(s\right) \mathrm{d} s \cdot \mathbf{A}\left(t\right)\) alakú felcserélhetőség, itt (a fenti \(f\left(t\right)\) mellett) azonban ez, könnyen ellenőrizhető módon, nem valósul meg.) Ezt már csak numerikusan tudjuk megoldani valamilyen alkalmas módszerrel (pl. Runge–Kutta-módszer). Ha megkaptuk a megoldást, akkor \(X_1\left(t\right)+X_2\left(t\right)+X_3\left(t\right)\)-ként adódik a retenciós függvény. Ezt, és az eredeti retenciós függvényt mutatja a következő ábra (itt már fontos hozzátenni, hogy az új retenciós függvény azzal a feltevéssel készült, hogy a beadás születéskor történik – hiszen itt már ugye nem mindegy, hogy milyen életkorból indulva számítjuk a raktározódást):
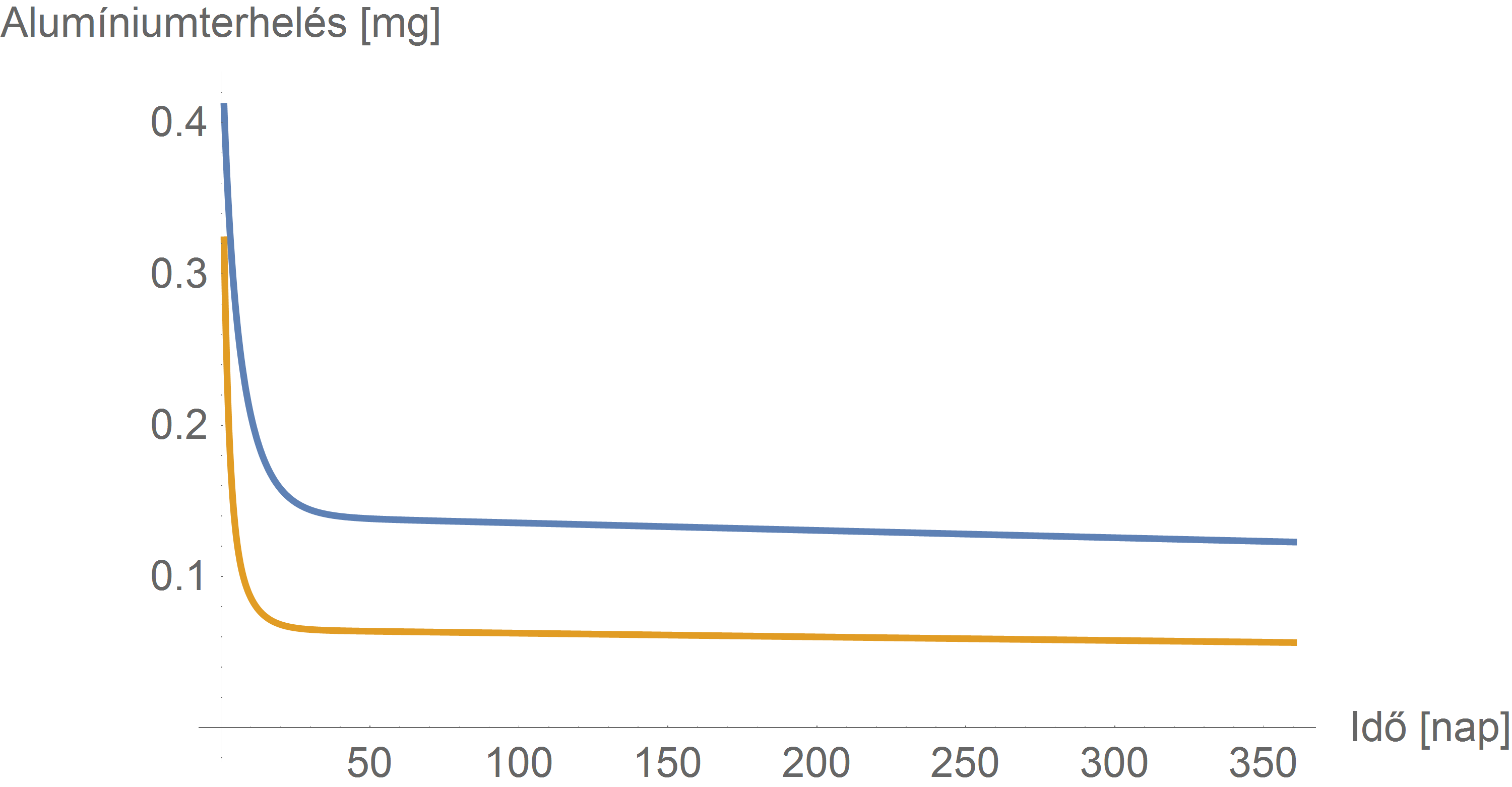
Látható, hogy az új feltételezések mellett – ahogy az várható is volt – az alumínium raktározódása nagyobb.
Persze az is sejthető, hogy nagyon hosszú távon a különbség csökken (szemben a fenti ábrával, ahol az időtartam rövidsége miatt nem látszik semmilyen közeledés), hiszen ezek a modellfeltevések épp azt jelentik, hogy a kiürülés idővel eléri a felnőttkorit. Ellenőrizzük ezt:
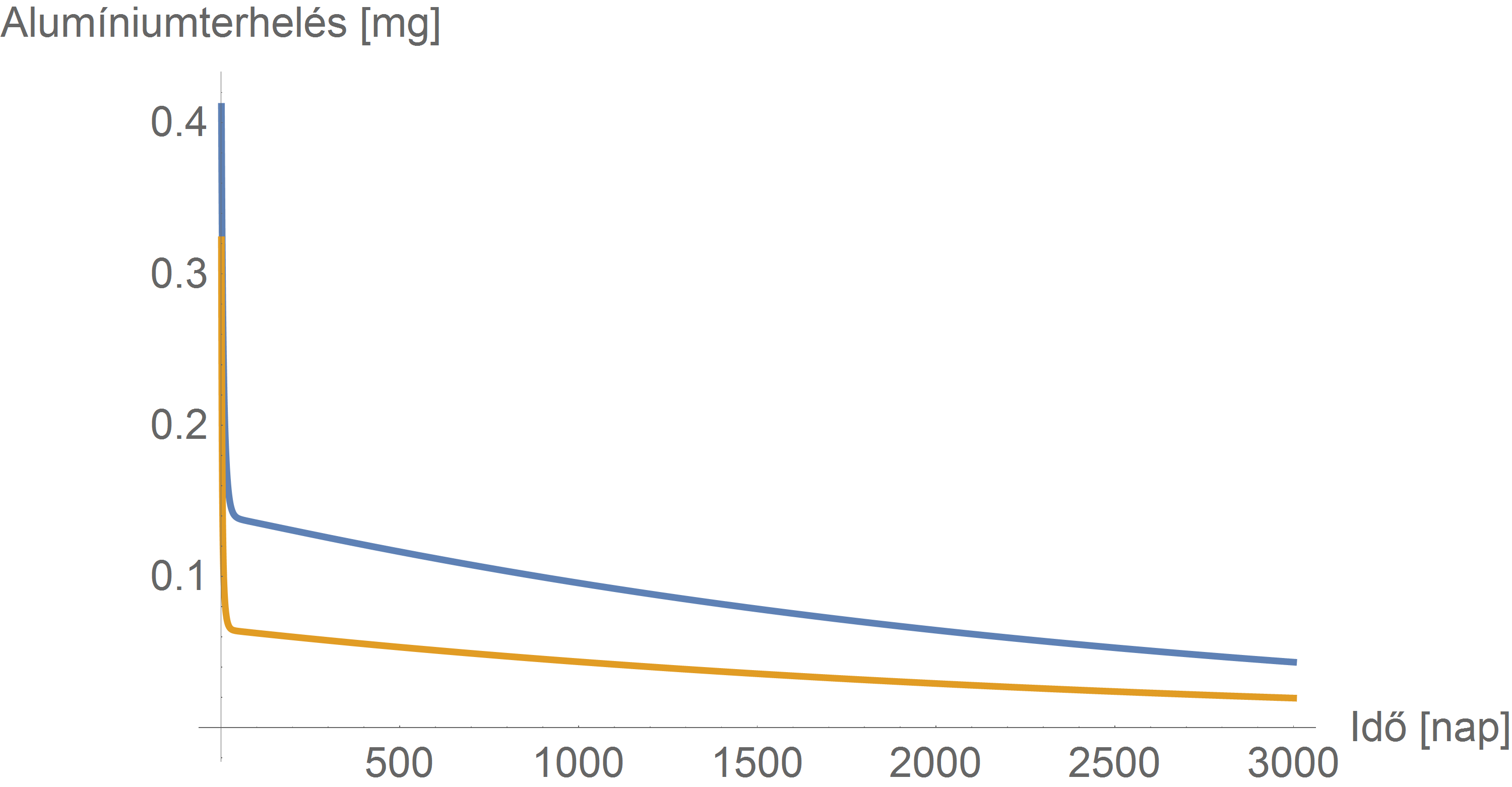
Látszik, hogy a várakozásunk teljesült, nagyon hosszú időt várva – az elért nagyobb kiürülés miatt – a két közelítés közti különbség eltűnik.
Most, hogy megvan az új retenciós függvényünk, azt ugyanolyan numerikus integrálásban (illetve egyszerű összegzésben) felhasználva kapjuk a végeredményt. Ezt mutatja a következő ábra:
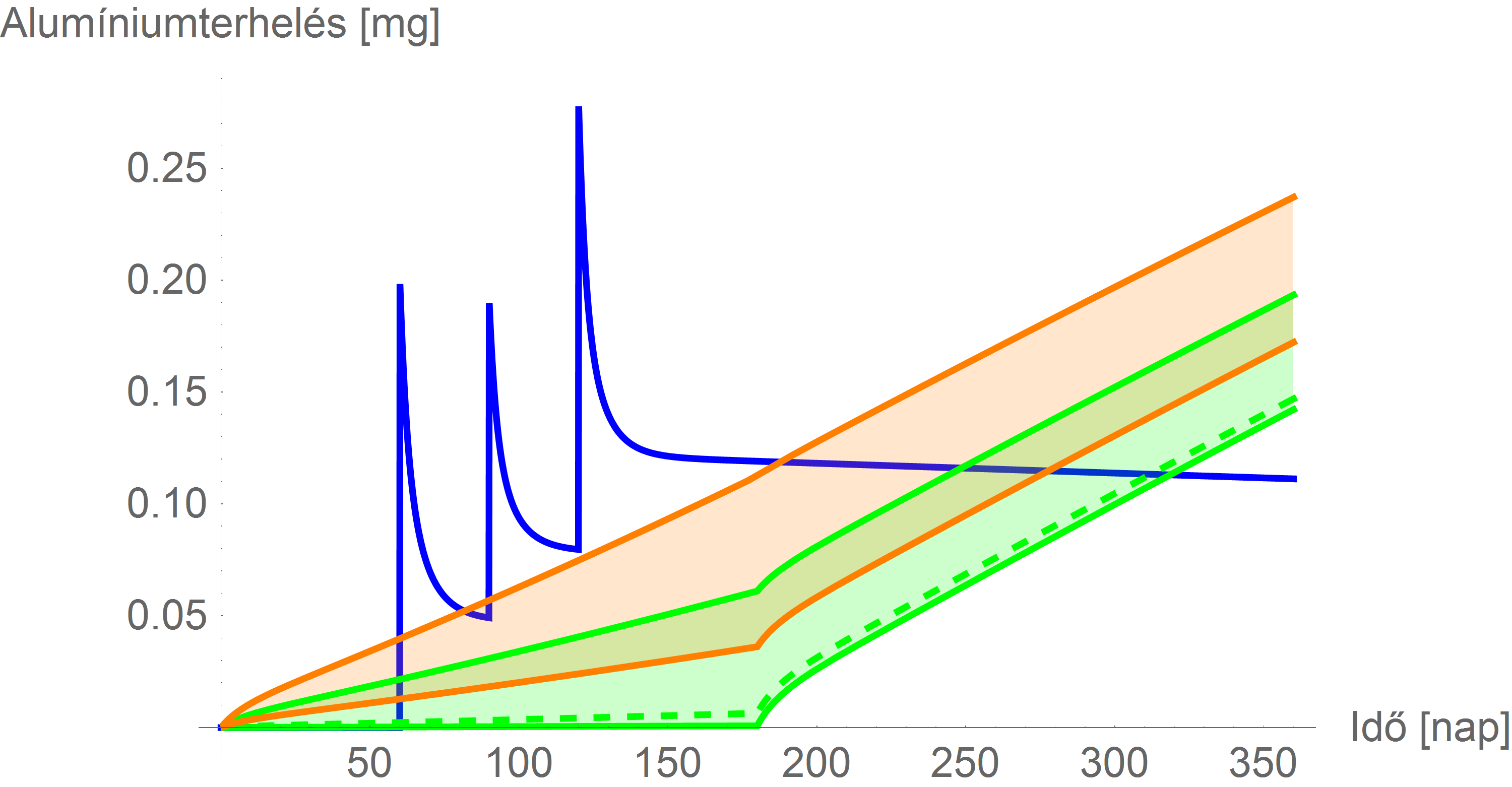
Látható, hogy mindkét forrásból (természetes és védőoltás) származó alumíniumterhelés is feljebb kúszott.
A limitekkel:
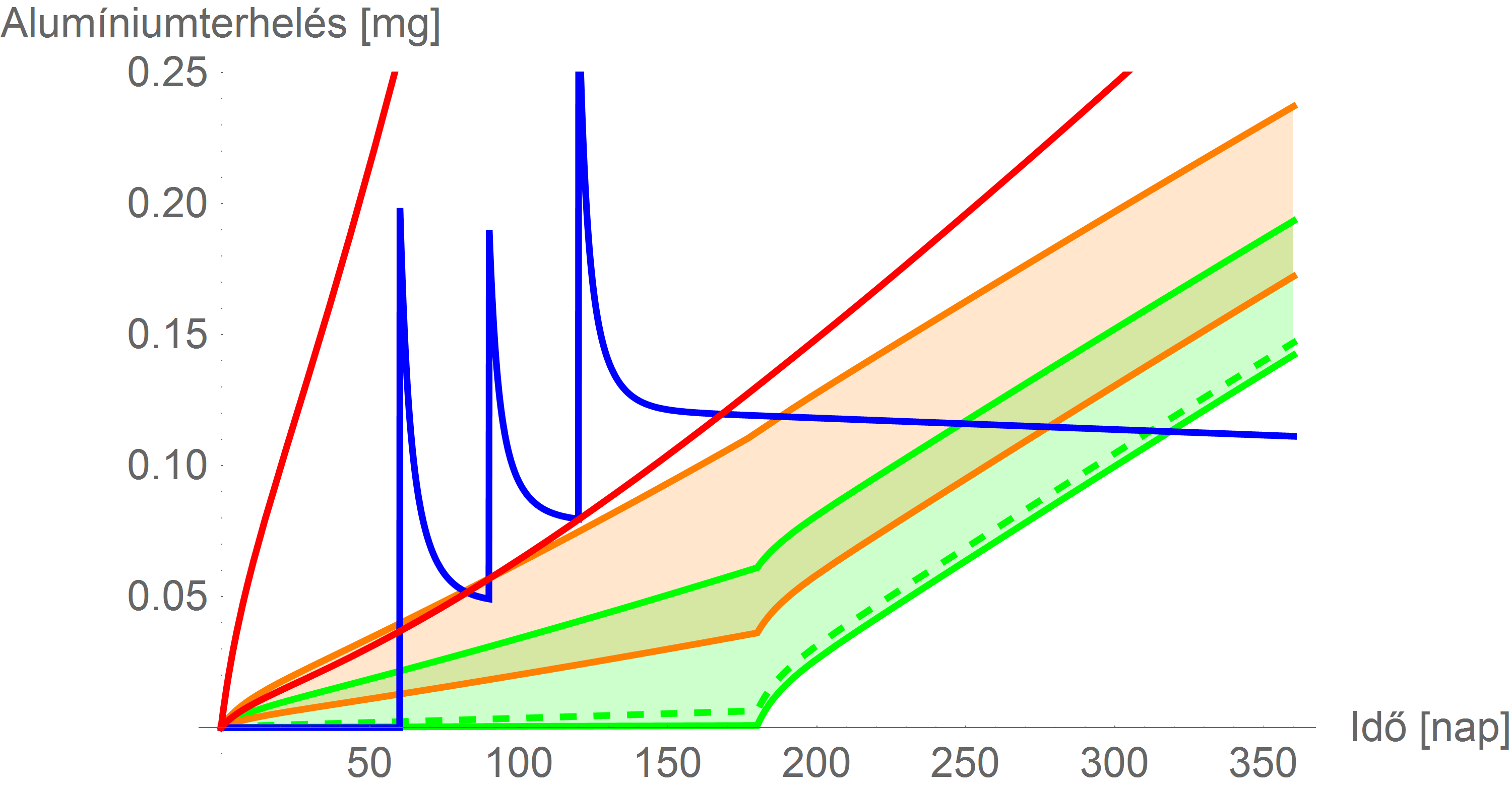
és
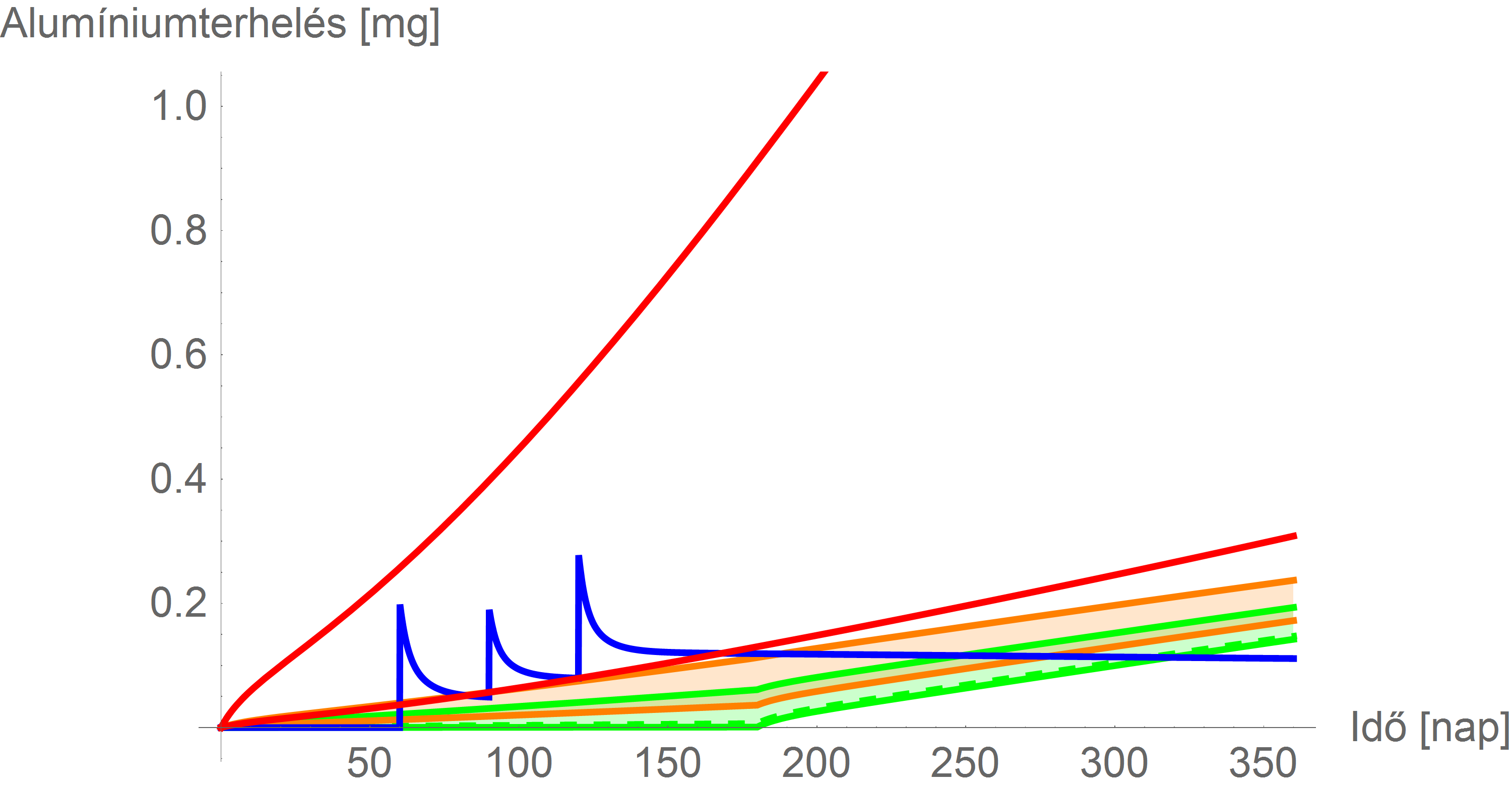
A magyarázat világos: az előbb említett effektus azt a bevitelt érinti legjobban, amelyik a legnagyobb mennyiségű – azaz a limiten történő táplálkozást. Ennek tudható be, hogy legjobban a piros vonalak emelkedtek meg (így a vakcinákból származó terhelés már a jelentősen szigorúbb korlátot is alig éri el).
Az injekcióban adott alumínium lokális felszívódása
Van egy második pont is, ahol ismét egy olyan feltevéssel éltem, ami megint csak durván rontotta a vakcinák biztonságát: azzal számoltam, hogy az oltással beadott alumínium azonnal, abrupt módon felszívódik, és teljes mennyiségében, késleltetés nélkül a szisztémás keringésbe kerül – ahogy azt az ábrákon lévő „tüskék“ is szépen mutatják. Noha ez a kinetikai számításokat nyilván lényegesen megkönnyítette matematikai szempontból, mindennek mondható, csak reálisnak nem (különösen, ha figyelembe vesszük, hogy az alumínium adjuvánsok használatának egyik oka épp az, hogy a lokális felszívódást elnyújtsák…). Kicsit precízebben: a védőoltásokban használatos alumínium adjuvánsok mind oldhatatlan alumínium sók, márpedig felszívódás és disztribúció csak azt követően várható lényeges mértékben, hogy a citrát-képződés révén oldható alumínium sók képződtek.
Szerencsére erre vonatkozóan vannak empirikus eredmények. Bár korlátozott erejűek (kismintásak és állatkísérletesek), de azért hozzávetőleges képet alkothatunk: egy kísérlet szerint az injekcióval, intramuszkulárisan (azaz izomba, tehát pontosan a védőoltásokkal megegyező módon) beadott, a védőoltásban találhatóval megegyező alumínium-hidroxid adjuváns mindössze 17 %-a került be a szisztémás keringésbe a vizsgálat 28 napja alatt! Az egyszerűség kedvéért tételezzük fel, hogy a felszívódás állandó rátájú (tehát \(\frac{0,17}{28}\) nap\(^{-1}\) ) mind a vizsgálat időtartama alatt, mind az után (tehát a teljes felszívódáshoz \(28/0,\!17=165\) nap kell).
Bár Mitkus és mtsai eredeti cikke e tekintetben csak ennyi elemzést végez, én egy nagyon picit továbbmentem: mivel a felhasznált paraméterben komolyabb bizonytalanság van (elsősorban az állatkísérletes forrás miatt), azt is kipróbáltam, amolyan érzékenység-vizsgálatként, hogy mi történik, ha a fenti felszívódási rátát felére csökkentem, illetve kétszeresére növelem.
Ezt figyelembe véve a természetes és mesterséges forrásokból származó alumíniumterhelés (utóbbinál a szaggatott a felhasznált paraméterrel, a két vastag vonal a fent részletezett alá- és fölébecslésekkel kapott eredmények):
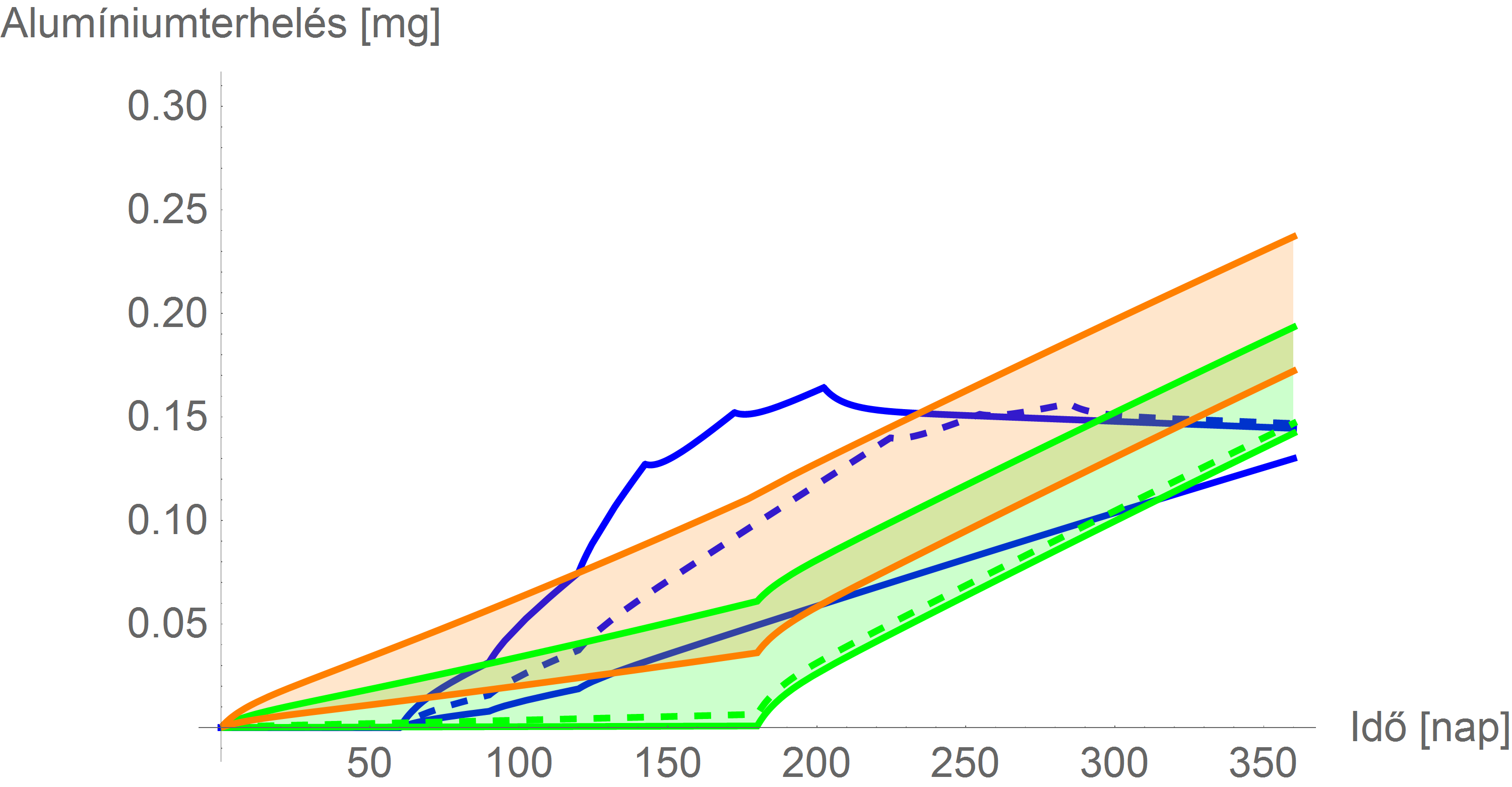
A limitekkel:
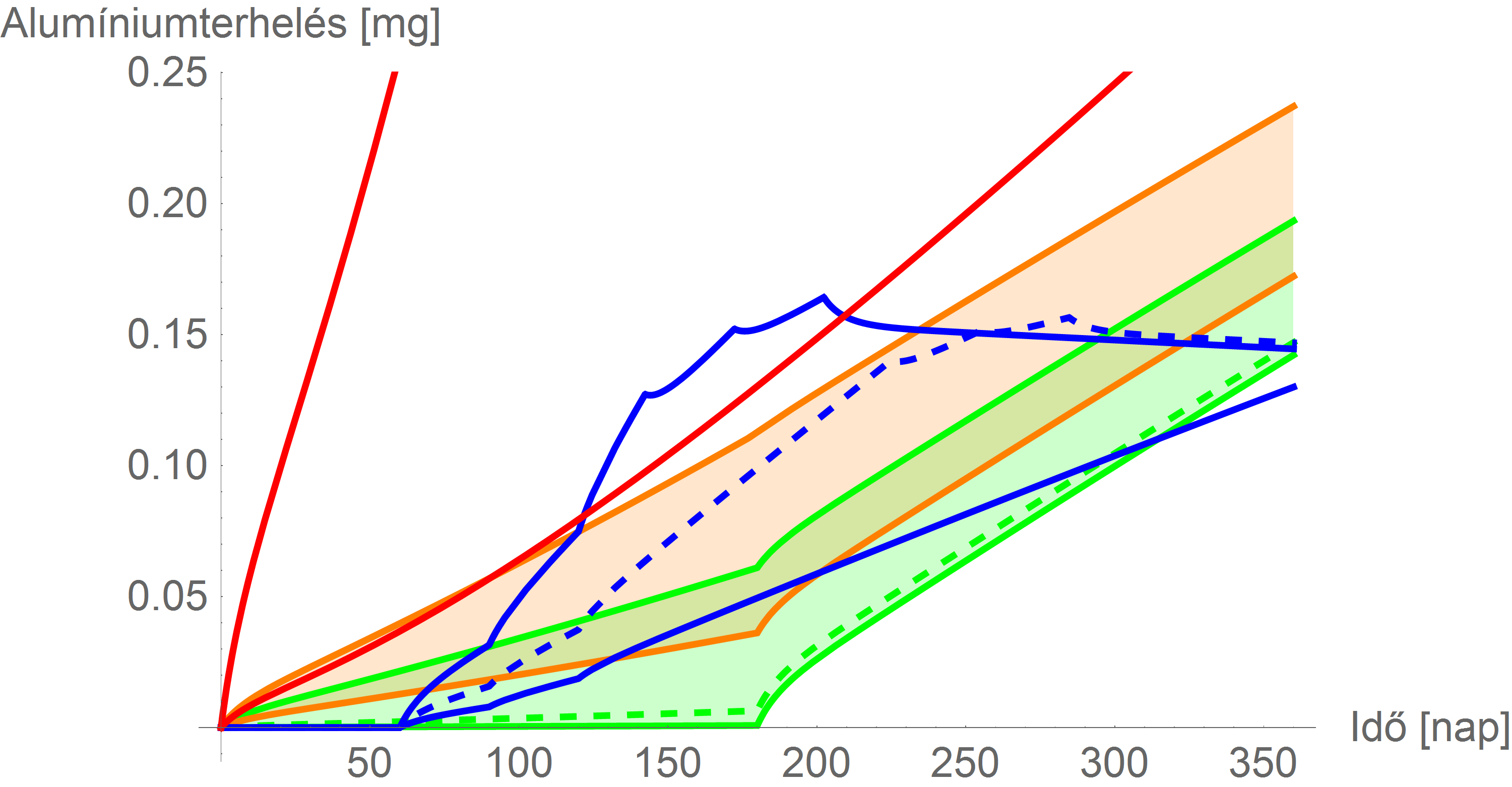
és
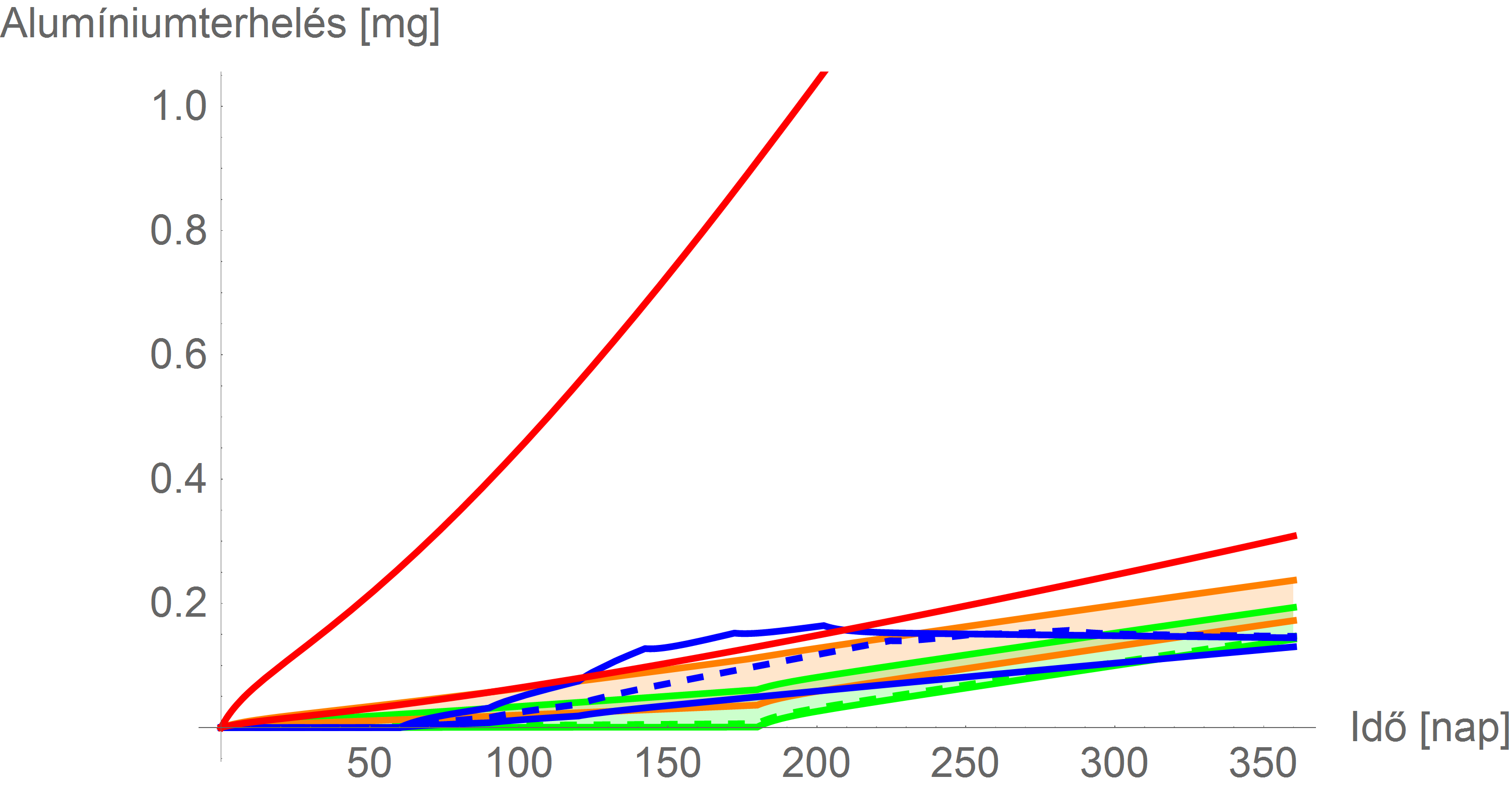
Születéskori alumínium-teher
Az alumínium minden ember szervezetének, így a várandós nőkének is természetes alkotója – ennek fényében nem meglepő, hogy az újszülöttek szervezetében már világrajövetelükkor is van alumínium. Az eddigi számítás ezt figyelmen kívül hagyta, így nagyon durván csaltam a védőoltások biztonsága ellen, hiszen ezt a – mint majd hamarosan látni fogjuk, egyáltalán nem elhanyagolható – mennyiséget „elfelejtettem“ feltüntetni a természetes terhelésnél.
Erre, mármint az újszülöttek szervezetének alumínium tartalmára vonatkozó közvetlen vizsgálat nincs az irodalomban, de olyan, ami újszülöttek vérszérumában mérte le az alumínium-koncentrációt, van. Eszerint az újszülöttek átlagos szérum alumínium-koncentrációja \(0,\!16\) \(\mu\)mol/l. Mivel a vérben keringő alumínium 90 %-a található meg a szérumban, így a teljes vér alumínium-koncentrációját kereken \(0,\!18\) \(\mu\)mol/l-nek vehetjük. (Ez jó egyezésben van a vér alumínium-koncentrációját közvetlenül kimérő vizsgálatok eredményeivel is.) Hasonlóképp továbbmenve, figyelembe véve, hogy a szervezetünkben található összes alumínium kb. 4 %-a van a vérben minden életkorban, azt kapjuk, hogy egy újszülött teljes szervezetének alumínium-koncentrációja \(4,\!4\) \(\mu\)mol/l. 3 kg körüli (jórészt vízből álló, így 1-hez közeli sűrűségű) újszülöttel számolva (itt most nem muszáj precíznek lennünk, e számítás többi hibaforrása úgyis nagyobb ennél), és figyelembe véve, hogy az alumínium moláris tömege 27 g/mol, azt kapjuk, hogy ez nagyjából \(0,\!4\) mg születéskori alumínium-terhet jelent.
Ezen \(0,\!4\) mg in utero terhelés sorsát illetően a vakcinák biztonsága szempontjából legrosszabb opciót választottam, azaz azt feltételeztem, hogy ugyanolyan retenciós függvény szerint ürül ki, mint egy intravénás bólusban beadott \(0,\!4\) mg alumínium.
Ezt figyelembe véve újra elkészíthetjük a fenti ábrát, hogy megkapjuk a következő, pontosabb eredményt (itt már a zöld és narancssárga területek és görbék jelentése természetesen nem „táplálkozásból származó“ alumíniumterhelés, hanem „természetes forrásból származó“ alumíniumterhelés, azaz a táplálkozásból származó és az in utero terhelés összege):
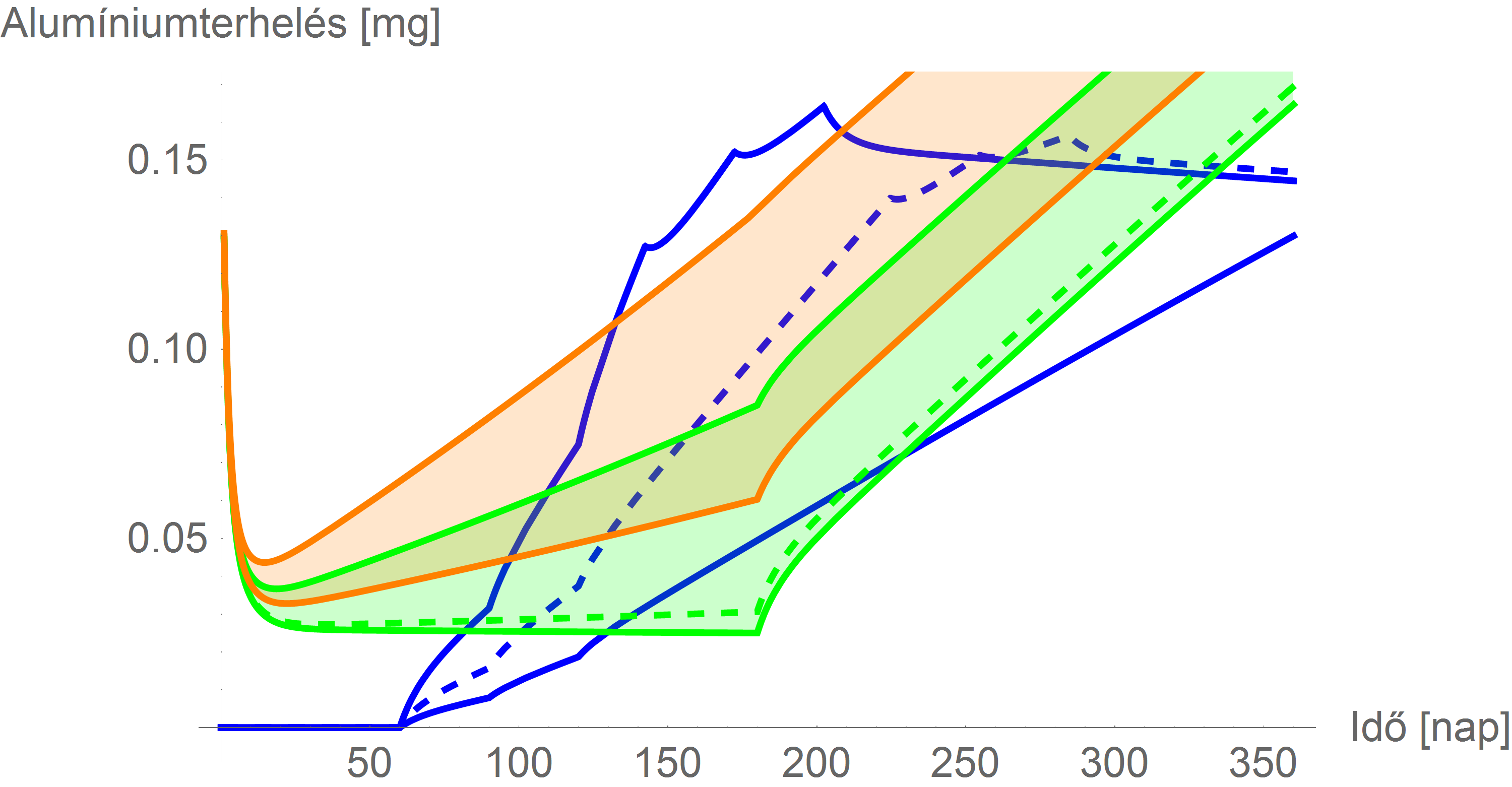
A limitekkel:
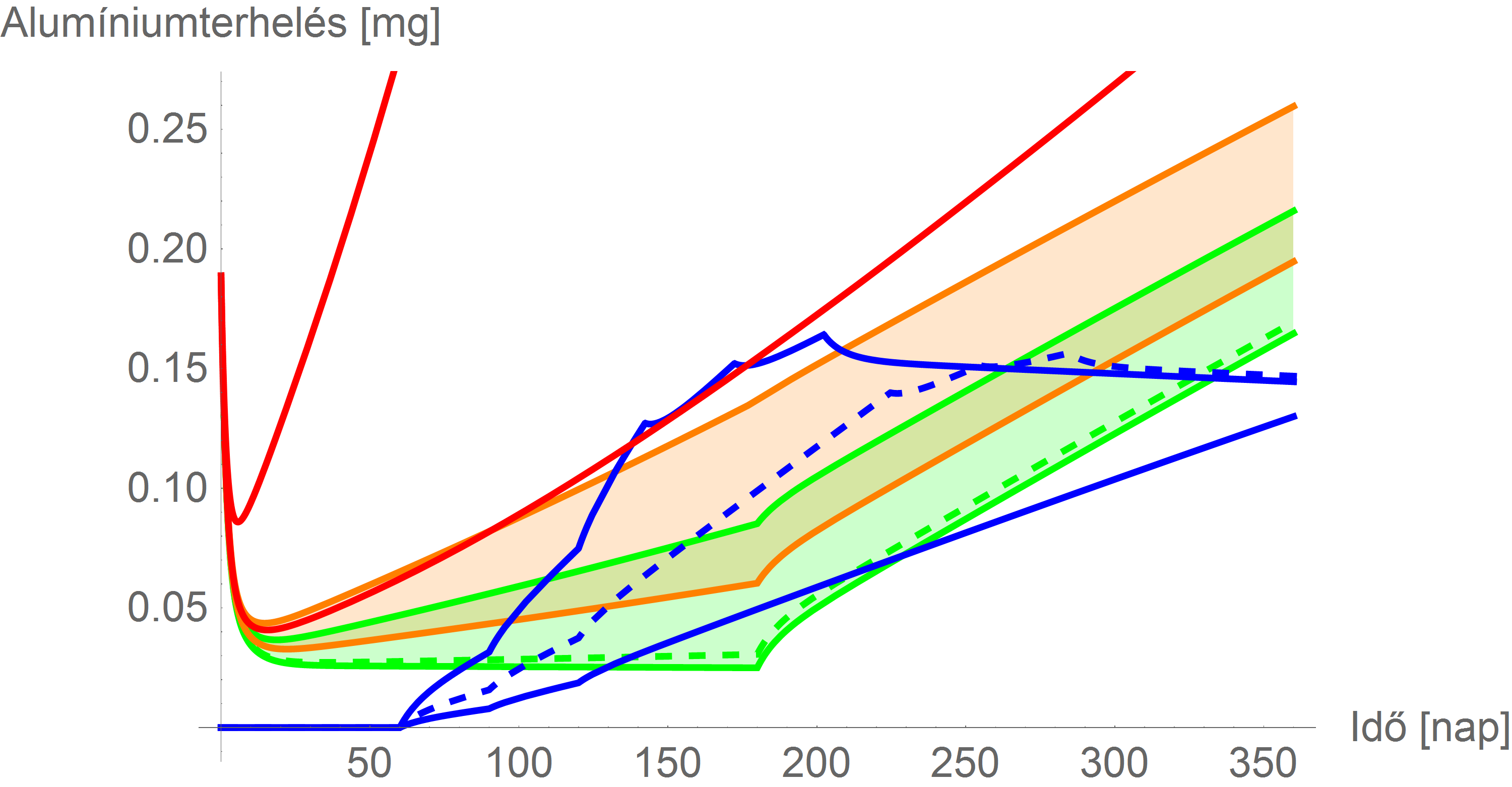
és
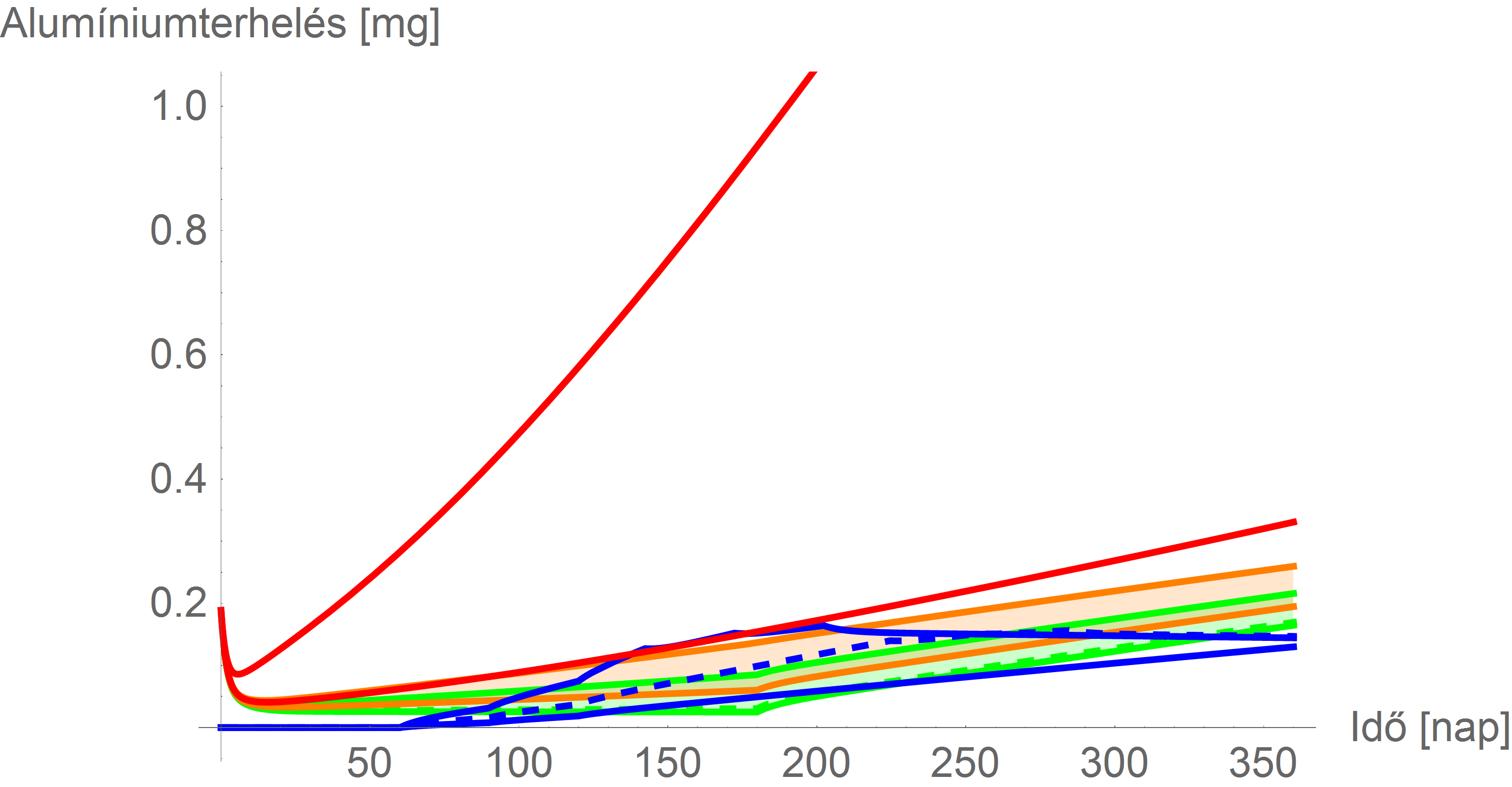
Konklúzió
Összefoglalóan megállapíthatjuk, hogy egy csecsemő életének első 60 napjában semmilyen alumíniumterhelésnek nincs kitéve a védőoltások következtében hazánkban; ezt követően pedig az oltásokból adódó alumíniumterhelés eleinte a természetes terheléssel összemérhető, az első életév után pedig egyenesen elhanyagolható mellette. (Ennek fényében nem meglepő, hogy a védőoltásokból származó alumíniumterhelés még a létező legszigorúbb, egész élethosszon át tartó folyamatos bevitelre megállapított limitet sem lépi át.) Márpedig a biztonság megállapításában ez a legszilárdabb fogódzkodó!
Mindezeket szemléltethetjük másképp is: tekintsük az első 18 év egészét! (Noha világos, hogy a gyermekek fejlődésében vannak kritikus időszakok, ezért igenis indokolt az ezekre fókuszáló elemzés is, de most, hogy ezt megtettük a fentiekben, nem felesleges kicsit bővítenünk a horizontot.) A következő ábra azt mutatja, hogy mennyi alumínium van egy gyermek szervezetében, ha a teljes kötelező oltási program összes védőoltását hiánytalanul, pontosan az oltási naptár szerint megkapja (piros görbe), és ha egyetlen egy oltást sem kap (kék görbe). Az ábra azzal a feltevéssel készült, hogy a táplálkozási alumíniumbevitel lineárisan éri el a felnőttkori 7 mg-ot (amivel még ugyancsak óvatos is voltam, hiszen így például az első év végi bevitel még csak 0,38 mg, ami a fele a valósnak...), továbbá figyelembe veszi, hogy a hepatitis B oltásokban más mennyiségű (0,5 mg a 0,3 helyett) alumínium van.
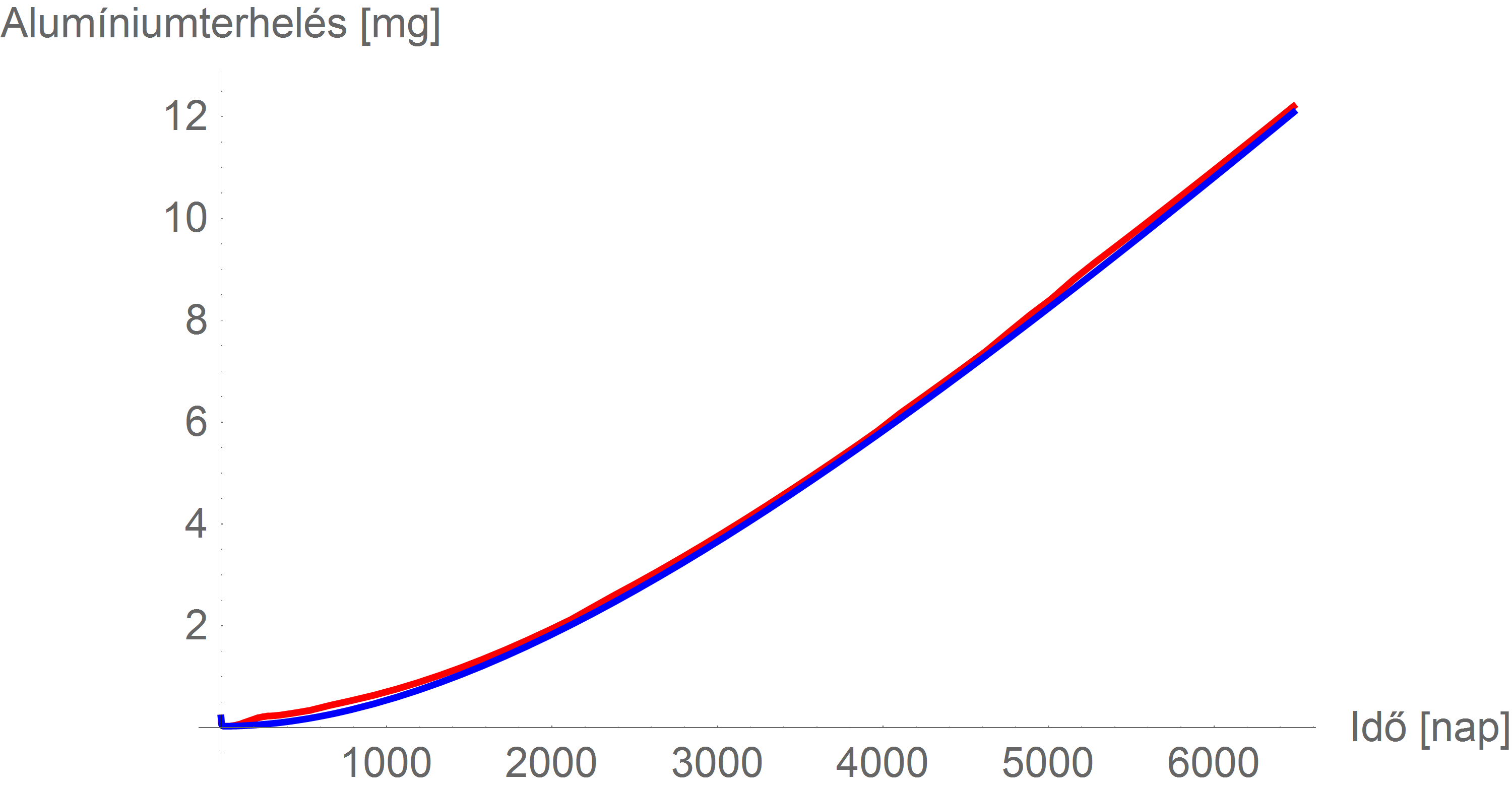
Emlékeztetőül: a kék görbe a védőoltás-ellenesek szerint az idilli állapot, míg a piros az, melyben a vakcinákból származó borzasztó alumíniumterhelés miatt ránk szabadulnak betegségek tucatjai autizmustól az epilepsziáig...
Viszont ha valaki netán napi 8 mg alumíniumbevitelig jut el, ugye ez még bőven belefér a táplálkozással történő természetes alumíniumbevitel mennyiségének természetes ingadozásába (sőt, ez még mindig a EFSA-szabvány alatt van, még egy 60 kg-os ember esetében is – noha említettem, hogy ez a szabvány olyan paranoiás, hogy az európai lakosság egy jó része kimondottan átlépi), akkor a szervezetében lévő alumínium mennyiségének alakulását a következő ábra szaggatott vonala mutatja (az előző ábrára vetítve).
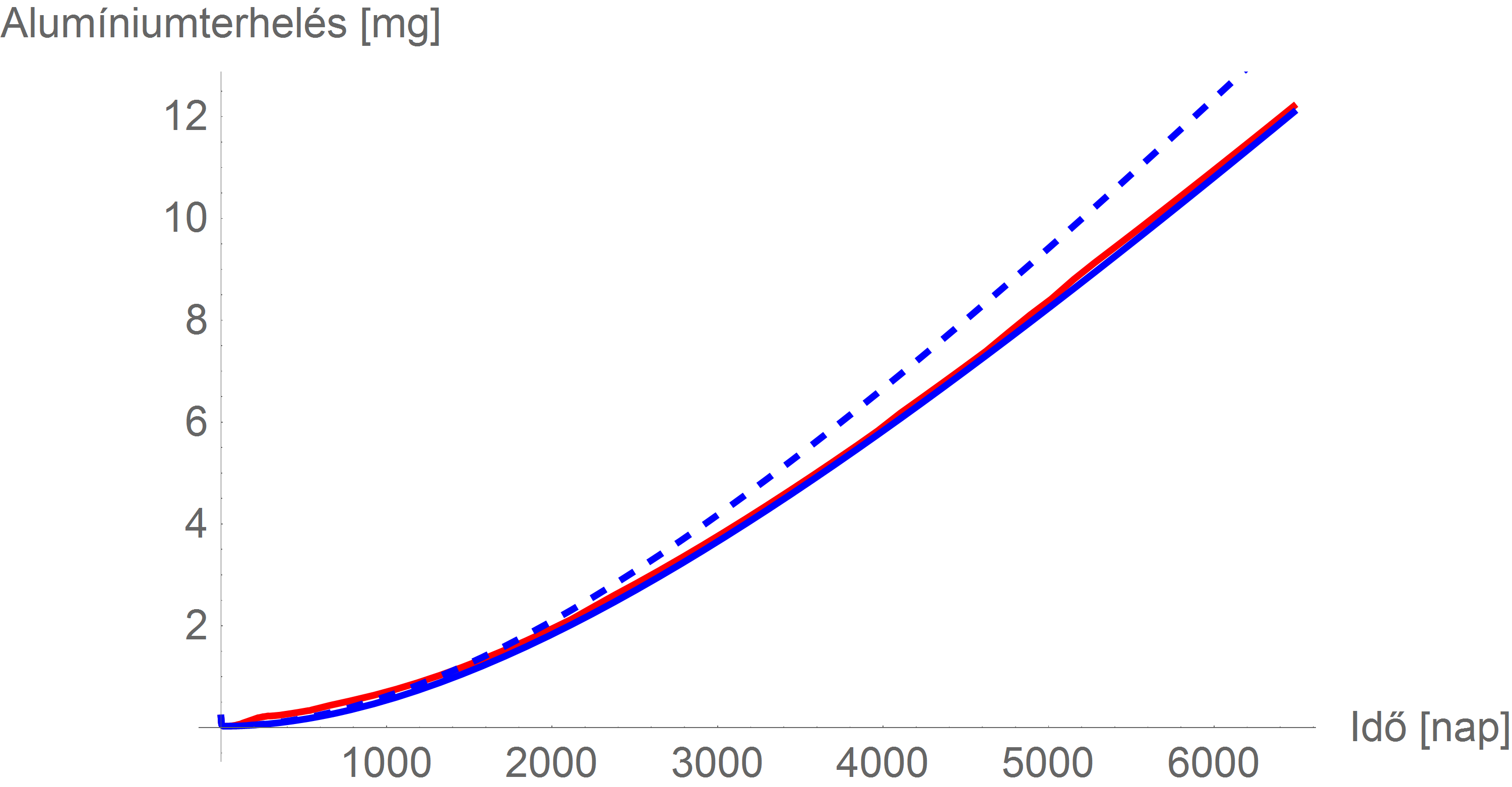
Azt hiszem, ez nem igényel további kommentárt.